The bellfounding firm of Gillett & Johnston of Croydon cast a considerable number of peals of bells and carillons from the early 1900s until the late 1950s when they exited the bellfounding business. Part of their success in bell founding was the work done by Cyril Johnston in the early 1900s to devise a bell shape and tuning techniques allowing the production of true-harmonic bells, in which three of the five lowest partials are in exact octaves. This gives true-harmonic bells a warm, musical sound.
G&J cast many peals of eight and ten, but only five complete peals of twelve. This paper investigates these peals to see what conclusions can be reached about how they were designed and tuned. Also included in the investigation is one peal where G&J augmented a Taylor ring to twelve – included to give additional insight into the design of the trebles. The peals are as follows:
| Place | Tenor | History |
| St Peter, Wolverhampton, West Midlands | 1,686kg, note Db – 34 | Cast 1911 |
| St Michael, Coventry, West Midlands | 1,717kg, note Db – 18 | Cast 1927 |
| St John, Croydon, Greater London | 1,875kg, note Db – 23 | Cast 1936 |
| St Philip, Birmingham, West Midlands | 1,584kg, note D – 32 | Back ten cast 1937, trebles cast 1949 |
| St Woolos, Newport, Wales | 1,101kg, note D + 34 | Back 7 Taylors 1913, trebles cast 1939 |
| St John, Halifax, West Yorkshire | 1,429kg, note D – 26 | Cast 1951 |
The bells at Coventry were the subject of the 1926 court case over replacement of the previous peal. They were originally installed as a chime, but as will be seen, were cast to ringing weights and have now been hung for ringing. The peal at Halifax was cast after Cyril Johnston left the business.
Musical scale / temperament used to tune the bells
In common with almost all Gillett and Johnston change-ringing peals, five of the six installations have nominals tuned Just. The exception is Coventry, where the bells are tuned in equal temperament. This temperament, used by G&J for their carillons, was used at Coventry because the bells were planned as a chime. Equal temperament allows music to be played in any key whereas Just tuning does not. Just tuning has the advantage that the frequencies are related by small whole-number ratios and so are easier to calculate. It is also suggested that Just tuning evens out the differences between tones and semitones.
Here are the theoretical intervals in cents relative to the tenor for the back eight of a twelve in the two tunings, including the two semitones provided at Coventry and the flat 6th provided at Croydon. Also given are the intervals taken from the tuning books for the as-shipped nominals – i.e. the frequencies actually achieved on the tuning machine, which are generally the same as those calculated as a target. The figures for Equal are the averages of Coventry and 14 equal-tempered carillons. The figures for Just are the average of 7 peals of bells. The bells chosen for the averages are those for which I happen to have the tuning book figures. The ± figures are the standard deviation.
| Bell | Equal – theoretical value | Tuning book nominal | Just – theoretical value | Tuning book nominal |
| 12 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 | 200.0 | 200.6 ± 2.4 | 203.9 | 204.9 ± 2.1 |
| 10 | 400.0 | 400.0 ± 2.4 | 386.3 | 387.8 ± 2.2 |
| 9 | 500.0 | 500.0 ± 1.7 | 498.0 | 498.5 ± 1.7 |
| 8 flat | 600.0 | 600.9 ± 2.5 | ||
| 8 | 700.0 | 700.4 ± 1.5 | 702.0 | 701.4 ± 1.2 |
| 7 | 900.0 | 900.8 ± 2.7 | 884.4 | 885.7 ± 2.1 |
| 6 flat | 1000.0 | 1000.3 ± 2.4 | 996.1 | 999.2 |
| 6 | 1100.0 | 1101.1 ± 2.4 | 1088.3 | 1088.0 ± 1.9 |
| 5 | 1200.0 | 1200.2 ± 0.8 | 1200.0 | 1199.8 ± 0.6 |
To put the discrepancies between tuning book figures and exact temperament in context, a difference of 0.5Hz (the closest to which frequencies are quoted in the books) is a difference of 3.2 cents at 273Hz, the hum frequency of the Chicago Rockefeller bass bell, and of 1.6 cents at 548Hz, the nominal frequency of the Coventry and Croydon tenors). These figures show very accurate tuning of the nominals. All the peals are tuned without stretch, i.e. the trebles are not sharpened relative to the tenors. Gillett and Johnston did stretch their carillons but only from the 3rd octave upwards.
Accuracy of nominal tuning
As can be seen from the previous table, the as-shipped nominals are very close to the desired temperament. The nominals actually measured in the bells today give a very different picture as seen in the following chart, which compares the measured nominals against the tuning book figures:
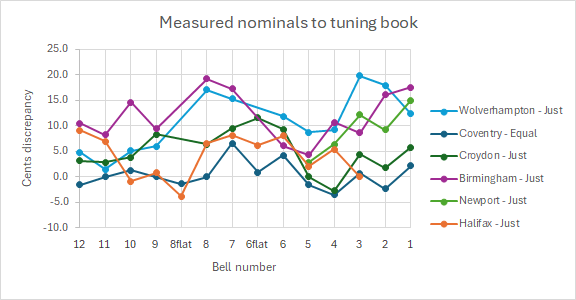
There are discrepancies of up to +20 cents and -5 cents, i.e. a total range of a quarter of a semitone. The range of variation for each peal means that the discrepancies are not due to recording speed or temperature effects. The explanation is errors in the tuning forks, as described here. The following chart shows the discrepancies in nominals and forks plotted against the note:
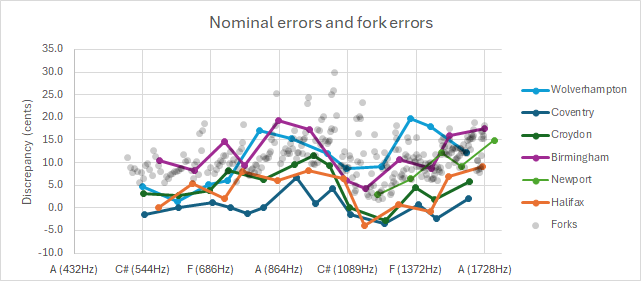
Obviously there is a big scatter in the fork errors, and the forks have significant outliers. But equally obviously, the variation in the nominals has a similar shape to the variation in the forks, and this is clearly the origin of the discrepancies. The curve for Wolverhampton, the first twelve cast and tuned in 1911 is broadly the same shape as those for later peals. The forks used to tune the Wolverhampton bells had the systematic errors shown by all G&J forks. I had previously thought that the first forks showing the errors were purchased in 1918 or 1919, as described on the page giving the history of the forks.
Other design aspects
In a letter from William Wooding Starmer to Taylors written in 1919 following a visit to the Croydon bellfoundry, Starmer says ‘Johnston has managed to get nearly a major 3rd in the tenor’. All G&J bells, in both ringing peals and carillons, have tierces that are sharp of equal temperament. The interval of the tierce to the nominal is set by the shape of the bell, especially near the soundbow, and is not amenable to alteration on the tuning machine. The following plot shows the tierce intervals in all the peals of twelve:

Apart from Wolverhampton, all the peals have consistent tierces at an average of 885 cents below the nominal. Equal tempered tierces would be 900 cents below the nominal, so the tierces in these bells average 15 / 100 of a semitone sharp of equal.
The tierces at Wolverhampton, the earliest peal, are quite different, and show a considerable gradient across the peal from 830 cents in the sharpest (the 11th) to 915 cents in the treble. The very sharp tierces in the tenors support Starmer’s statement above. The sharp tenor tierces make these bells sound unlike peals with more conventionally tuned tierces.
The interval between octave nominal and nominal in bells gives important clues as to design – proportionally thicker, heavier bells have flatter octave nominals. The following chart shows the octave nominal tuning across all six peals:

With the exception of Wolverhampton, all the peals show a steady gradation between tenors and trebles, evidence of consistent design. The octave nominals at Wolverhampton are quite different, clear evidence that this peal was an early experimental effort. The trebles at Birmingham and Halifax have the flattest octave nominals, so these bells are proportionately the thickest and heaviest across all six peals. This is further emphasised by the following chart, which shows the relative weight of all bells against the tenor of the peal:

Unlike the octave nominals, the weights of the Wolverhampton trebles are not anomalous. Setting aside Newport, where the trebles were added to existing Taylor tenors, the heaviest trebles are, in order, Halifax, Birmingham, Croydon and Coventry. The relative weight of G&J trebles steadily increased as the years went by, done to improve the ease of ringing and striking the trebles.
Acknowledgements
I am grateful to David Bagley for recordings of Wolverhampton, to Mike Chester for recordings of Coventry, and Andy Parry for recordings of Newport. Chris Pickford and Kye Leaver provided the extracts from the Gillett & Johnston tuning books.