Bell weights, diameters and frequencies are obviously related; heavier bells sound a deeper note, and heavier bells are generally bigger in diameter. But are there any quantitative rules that allow, say, a bell’s weight to be estimated from its diameter and partial frequencies? Partial tones and bell diameters are generally easy to measure or are published. Bell weights on the other hand cannot be measured without substantial lifting and weighing equipment, and permission to weigh a bell in the tower is very unlikely to be granted unless other work is in progress. So it is useful to be able to estimate the weight of a bell from other data. A subsidiary question of interest is whether steel bells are lighter than their bronze equivalents.
Although it is all we have, published information on bell weights is not always of the best quality: the weight of bells can be exaggerated, weights can be estimates, and canons may or may not have been removed from older bells. But as will be seen, conclusions can still be drawn.
Bells with the same note can have a range of weights. As an example, compare the tenors of the peals of 10 at Derby Cathedral and Wells Cathedral. Wells Cathedral tenor has a weight of 56cwt 1qtr 14lbs or 2,864kg and sounds the note C. Derby Cathedral tenor has a weight of 19cwt 0qtr 1lb or 966kg and sounds the note Db – only a semitone higher and 1.9 tonnes lighter.
The smaller bells in both ringing peals and carillons are designed heavy in proportion to the tenors / bass bells to give them more power, in the case of ringing bells to give them better mechanical characteristics, and in the case of small carillon bells to make them big enough to fit the clapper inside. And although heavier bells in general have a lower nominal frequency, when a bell is tuned its weight goes down but often its nominal goes down as well.
Charts of weight, diameter and nominal frequency
To demonstrate the relationship between bell nominal frequencies, diameters and weights the plots below cover 7,165 bells with weights ranging from 1.84kg (bell number 2 in David Bagley’s private ring in Tewkesbury) to 71,800kg (the heaviest bell at Trinity Lavra, Sergiyev Posad, Russia). 193 of the bells are steel bells. The bells span nine centuries and hundreds of founders. Weights are plotted in kilogrammes and diameters in metres. All the plots are log plots using natural logarithms.
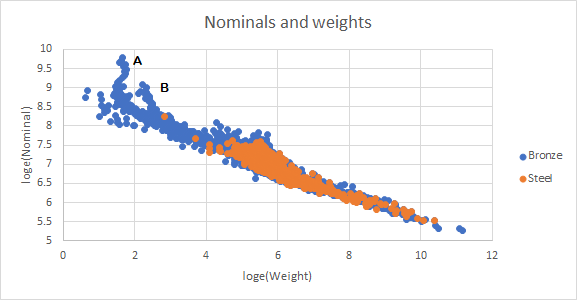
The first plot of nominal frequency against weight shows there is a primary linear relationship but with significant excursions. The set of bells marked A comprises the treble bells at the Rockefeller Memorial Carillon in Chicago, cast by Gillett and Johnston in 1931. The top 22 bells of this carillon are fundamentally the same weight, ranging between 4.5kg and 5.8kg, not in order of nominal, while their diameters increase steadily from 13.5cm to 19.7cm. The set of bells marked B are the trebles of the carillon at Ghent, cast by Eijsbouts in 1981 and 1993. The smallest 12 bells have weights between 9.21kg and 12.1kg, again not in order of nominal, while the diameters increase steadily from 20cm to 24cm. The set of bells with high nominals for their weight between 4 and 5 on the X-axis are the trebles of ringing peals and chimes, case heavy in comparison with their tenors.
There is nothing in this plot to suggest steel bells follow any different pattern, and the weights of steel and bronze bells for the same nominal frequency are comparable. This assertion will be quantified below.
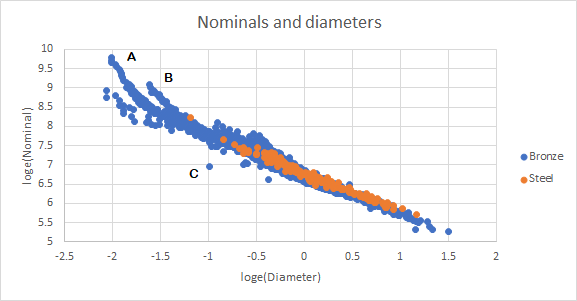
The plot above of nominals and diameters follows a similar pattern. The sets of bells marked A and B are the same carillon bells as above. The bell marked C is a bell by Van Den Ghein cast in 1615, featured by André Lehr in a paper published in 1986, and no doubt chosen for its unusual design. The bells above the line between -1 and 0 on the X-axis are again the trebles of rings and chimes designed big in proportion to their tenors.
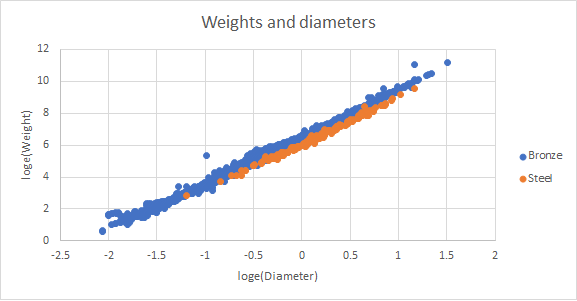
This last plot of weights and diameters completes the picture, and it is the nearest to a straight line. There are no major excursions for carillon bells or trebles, because when a bell is cast proportionately heavier, its diameter has to be increased to maintain the same nominal frequency. The outlier at -1 on the X-axis is again the 1615 Van Den Ghein bell. It is clear from this plot that steel bells are consistently lighter than bronze bells of the same diameter.
Regressions and formulas to estimate bell weight in steel and bronze bells
Ben Kipling in a recent article in The Ringing World (issue 5773-5, 17-31 December 2021, page 1187) explains his use of a formula
W ≈ k.f.d4
where W is weight, k is a constant for a given profile (which he gives as typically about 0.74kgsm-4 for a modern change-ringing bell), f is the frequency of the nominal, and d is the diameter. His formula gives good results but the constant k needs to be adjusted for bells of different profiles.
A regression fit for the 7,165 bells in this analysis, gives the following formulae:
w ≈ 0.927 f0.96 . d3.87 for bronze bells
w ≈ 0.623 f0.96 . d3.87 for steel bells.
The constant k for bronze bells is higher than that given by Ben in his article because the powers of f and d are different, and many of the bells in this sample are not change-ringing bells.
The formulae above suggest that for a given nominal and diameter, steel bells will be 67% of the weight of a bronze bell. This quantifies the difference shown in the final plot above.
Investigations into the effect of other partials such as the hum, prime, tierce and octave nominal on bell weight suggest that none of them provide a good explanation of remaining variances. These investigations give rise to a range of models which all have the form fp x dq where q – p is always just less than 3. This standard form arises because the nominal frequency and diameter of a bell are related quantities, as the second plot shows.
Another pair of formulae based on a regression fit forcing p = 1 and q = 4 gives the following:
w ≈ 0.715 f . d4 for bronze bells
w ≈ 0.466 f . d4 for steel bells.
Again this pair of formulae suggest that steel bells will be 65% of the weight of a bronze bell with the same nominal and diameter. The different constant (0.715 compared with Ben Kipling’s 0.74) is no doubt due to the fact that many of the 7,165 bells do not have a change-ringing profile.
A further regression, this time of log(weight) against log(nominal) only, ignoring the diameter gives the result that a steel bell will weigh 96% of a bronze bell with the same nominal. So to a good approximation we can say that bronze and steel bells with the same nominal will weigh about the same. Their diameters of course will be different.
The weight of steel bells
It is sometimes said that for the same note (i.e. nominal frequency), a steel bell will be lighter than a bronze bell. As there is a trade-off between weight and diameter chosen by the bell designer, this is actually a comment on the typical shapes, diameters and thicknesses used for bronze and steel bells.
The first plot above of nominal frequency against weight shows that the weight of bronze and steel bells for the same nominal frequency is very comparable. The regression mentioned in the previous paragraph confirms that for the same nominal, a steel bell will weigh 96% of its bronze equivalent.
The last plot of weight against diameter shows that, for the same weight, steel bells tend to have a larger diameter than their bronze equivalents. A regression shows that, for the same weight, a steel bell typically has a diameter 12% greater than its bronze equivalent.
Re-arranging the formulas above to derive a value for k we have either:
k = w . f-0.96 . d-3.87 or k = w . f-1 . d-4
We can use the ratios of weights and diameters to calculate the ratio of the k’s for bronze and steel bells, and from the two formulas get a ratio of 0.67, or 0.66. These are the same values as derived above, which confirms the analysis.
So to summarise the difference between bronze and steel bells, for bells with the same nominal:
- The weight of the steel bell will typically be 4% less
- The diameter of the steel bell will typically be 12% greater.