This paper is one of the two key papers investigating the modes of vibration of bells, the other being Perrin, Charnley and DePont’s paper Normal Modes of the Modern English Church Bell. As this paper by André Lehr is not reprinted in Rossing’s Acoustics of Bells, it is provided here. The partial classification scheme is the same as the one proposed by Lehr in his 1965 paper.
This 1986 paper gives the practical bellfounder’s view of modes of vibration, and includes analysis of a number of bells including some specially cast for the investigation.
André Lehr
Royal Eijsbouts Bell Foundry, Asten, The Netherlands
From Journal of Acoustic Society of America 79(6), June 1986, pp. 2000-2011
(Received 9 May 1984; accepted for publication 11 February 1986)
Abstract
The flexural vibrations of a bell can be classified into different groups, each group consisting of partials with an equal number of nodal circles in about the same position on the bell wall. A bell also shows extensional vibrations which seldom occur at frequencies below the nominal, except in carillon bells with a thick wall. These vibrations are sometimes important for the timbre of the bell in spite of the fact that their amplitudes are usually small because extensional vibrations have an antinode at the head of the bell. Research into the dependence of partial frequencies on wall thickness did not support the linear function predicted by the elementary bending theory. Measurements on especially designed bells that differed only in wall thickness were more consistent with an extensive theory of, e.g., a ring. Partials were found to shift in groups, not individually, as a function of increasing wall thickness. From a musical viewpoint, the group of flexural partials with a nodal circle at the waist of the bell is important in forming the bell’s primary and secondary strike notes. The bell’s timbre will depend on relative partial amplitudes, the partial intervals within groups, and the position of partial groups with respect to one another.
Introduction
It is customary in campanology to deem the tuning of a bell as completely described by the frequencies of the first five partials. This is insufficient, however, for understanding the physics of bell vibrations. It has been known for a long time that the sonority of a bell is judged by the relationship between frequencies, intensities, and decay times of partials. When judging a bell by its sound qualities, the higher overtones or “mixture tones” are only indirectly considered. The total impression is apparently dominated by the base chord, so one can understand why the lower partials are tuned to a musical series. The minor triad in the form C4-C5-E5♭-G5-C6-G6 is mostly used, with the hum note stated as C4. This corresponds to the frequency ratios 5:10:12:15:20:30 or 1/12:1/6:1/5:1/4:1/3:1/2. This should be considered an ideal tuning, and differences with actually obtained frequencies will depend on the skill of the bell founder. Because this type of bell, the minor octave bell, can be formed in many ways, two design factors must be considered as most important.
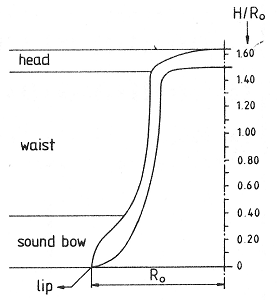
FIG. 1. One half of a longitudinal section of an arbitrary bell profile.
In the first place, there is the model. Figure I shows one half of a longitudinal section of a given profile whose most important feature is its thickness function. The thickest part near the mouth of the bell, the sound bow, plays an essential part in forming the tone. This is the place where the clapper strikes. Bell profile and bronze characteristics are other important factors that determine the frequencies, the relations between them, and the decay times of the various partials. A second important characteristic is the size of the bell. Usually this is given by the largest radius R0. For a given profile, R0 determines the pitch or tone of the bell. By the principle of dynamical similarity, this is expressed as
(1) fR0 = k
in which f is the frequency of the hum note (or any other partial), and k is a constant for a series of similar profiles. When a number of ringing bells are cast in the bell foundry, they are usually derived from one standard bell with the aid of Eq. (1), resulting in variations in absolute dimension only and not in model. It is remarkable that nearly every founder of any age takes values of k around 100m/s forthe hum note. This is apparently considered the ideal bell, regardless of details of bell material or profile.
The weight can be calculated with the formula
(2) M = cR03
in which M represents the mass and c is a constant for a certain type of profile that can be calculated from the dimensions and the weight of the standard bell. The practice of designing a series of ringing bells is therefore quite simple.
With carillon bells, however this is quite different. A carillon consists of a series of bells with a progression of pitches tuned to a chromatic scale. When Eq. (1) is applied to these bells, the highest bells will become unreasonably small. If, for example, the lowest bell of a four-oct carillon has C3 (130.8 Hz) as hum note and 0.8m as R0, the smallest bell, with a hum note of C7 (2093 Hz), will have a radius R0 of 0.05 m. It is therefore customary to increase the bell’s dimensions relative to the scaling of Eq. (1) when the tone becomes higher, which leads to a thicker wall. This is expressed by a gradual rise of the constant k over the scale. Personal preference of the designer defines the extent of the increase in k, so it is rather difficult to give general rules. It appears, however, that the early 16th century bell founders applied only very slight increases in the factor k, so a bell with hum note C6 (1046Hz) would have a maximum k value of 250m/s. In later years one notices a clear tendency to increase k values considerably. This was particularly stimulated by the present-day bell founder’s ability to cast bells of relatively high pitch, with hum notes of C7 or even G7. For the latter bells, 400-500 m/s is usually taken as ideal k value. Only in this way does one obtain treble bells that are correctly related to the large bells in sound intensity and sonority.
These introductory remarks especially pertain to what is musically noticeable in a bell. The following exposition will show that the knowledge of physical bell properties provides further insight into the musical facets of the bell sound. Two fundamentally different types of vibration modes, the flexural and extensional modes, are described in Secs. I and II. In Sec. III the results of an experiment are discussed in which the dependence of these two types of modes on wall thickness was systematically investigated. Musical consequences are discussed in Sec. IV.
I. Flexural Modes
A. General Remarks
Flexural modes are oscillations in which the restoring forces are forces norrnal to the bell surface which result from the bending stiffness of the bell wall. To obtain a complete picture of a vibrating bell, it is necessary to measure three displacement functions for each partial, corresponding to the three dimensions in which the bell vibrates. Because tangential displacements do not radiate very efficiently, contribute little to the sound of the bell, and are also very difficult to measure, only radial displacements are considered here. Even measuring all radial characteristic functions is such an extensive task that only radial node patterns for each partial are considered. It is true that with this approach the wall amplitudes will be known only approximately and that the relation between maxima will remain completely unknown, but nevertheless the number of nodes and their positions provide sufficient information for a first study on the character of partials and their classification into groups.
In the theory of vibrating plates, cylindrical and conical shells, etc., it is possible to determine partial groups of flexural vibrations, each group characterized by some common characteristic. Such a characteristic can be the number of nodes. For example, in the first approximation of the frequencies of a freely suspended round plate of constant thickness calculated by Kirchhoff (Rayleigh, 1877), the factor (s + 2m) occurs, where s is the number of nodal meridians and m the number of nodal circles. Obviously it is possible to compile series of frequencies with the same number of nodal circles and increasing number of nodal meridians. The same can be said for a cylinder and a cone, and should hold for a bell as well. It will be shown, however, that for a bell the definition of a group needs to be extended, since the mere number of nodes is not sufficient to identify a group. Therefore, we will identify a group as a collection of partials with the same number of nodal circles in approximately the same position on the bell surface. In order to obtain a division of partials into groups, one needs to know the frequencies and the number of nodes for each partial.
B. Measurement techniques
An RC tone generator, amplifier, and an electrodynamical vibrator (Philips) were used for measuring natural bell frequencies. Each frequency could be determined with an accuracy of +-0.2% or 3 cents. In order to bring the bell into resonance, one has to press the pin attached to the moving coil of the vibrator against the bell at a place where the driving point impedance is low. This will add a small mass to the bell wall, but since the moving mass of the vibrator is only 3g, the error introduced in the observed resonance frequency will be very small. This pin is also attached in such a way that “buzzing” against the hard wall of the bell does not occur.
With this electric excitation system one can make the bell sound any particular mode continuously. One can then easily determine the nodes, for instance, by means of a microphone held close to the bell’s surface (van Heuven, 1949). The microphone signal will show maxima and minima at antinodes and nodes, respectively. A suitable variation to this method is to use the vibrator as a pickup. In that case there is immediate contact with the vibrating bell wall, eliminating the need for acoustic conduction.
A third method is using a stethoscope. The bell surface can easily be scanned by this instrument, enabling aural determination of the nodal pattern. Finally, one can make use of the fact that it is impossible to set up a particular resonance by excitation at a node. Naturally, this method lends itself only to determination of nodal circles. Throughout the experiments, all four methods were used independently with similar results.
C. Results
| Height (H/R0) of the nodal circles | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Musical name | Note | Cents to nominal | f (Hz) | s | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | m = 6 | Notation for flexural partials | |||||
| Hum note | F3 – 43c | -2402 | 170 | 2 | 1.58 | |||||||||||
| Fundamental | F4 – 41c | -1200 | 341 | 2 | 0.36 | 1.51-1.58 | ||||||||||
| Minor third | A4♭ – 27c | -886 | 409 | 3 | 0.64 | 1.48-1.58 | I-3 | |||||||||
| Fifth | C5 – 36c | -495 | 512 | 3 | 0.21 | 1.58 | II-3 | |||||||||
| Nominal | F5 – 41c | 0 | 682 | 4 | 0.62 | 1.56-1.58 | I-4 | |||||||||
| F5# – 9c | 132 | 736 | 1 | 0.27 | 0.96 | |||||||||||
| Major tenth | A5 – 7c | 434 | 876 | 4 | 0.22 | 1.32-1.58 | II-4 | |||||||||
| 1st eleventh | B5♭ – 81c | 460 | 890 | 2 | 0.21 | 0.69 | 1.47-1.58 | III-3 | ||||||||
| 2nd eleventh | B5♭ – 46c | 495 | 908 | 3 | 0.21 | 0.69 | 1.49-1.58 | III-3 | ||||||||
| B5 – 8c | 633 | 983 | 1 | 0.23 | 1.29 | |||||||||||
| Twelfth | C6 – 34c | 707 | 1026 | 5 | 0.74 | 1.34-1.58 | I-5 | |||||||||
| Thirteenth | D6 – 64c | 877 | 1132 | 4 | 0.21 | 0.73 | 1.48-1.58 | III-4 | ||||||||
| D6 + 45c | 986 | 1206 | 1 | 0.21 | 0.57 | 1.29 | ||||||||||
| Fourteenth | E6 – 39c | 1102 | 1289 | 5 | 0.20 | 1.35-1.58 | II-5 | |||||||||
| E6 + 4c | 1145 | 1322 | 1 | 0.23 | 0.84 | 1.36 | ||||||||||
| Double octave | F6 + 32c | 1273 | 1423 | 6 | 0.87 | 1.52-1.58 | I-6 | |||||||||
| F6 + 34c | 1275 | 1425 | 2 | 0.18 | 0.47 | 0.91 | 1.41-1.58 | IV-2 | ||||||||
| F6♭ – 35c | 1306 | 1450 | 3 | 0.22 | 0.47 | 0.91 | 1.40-1.58 | IV-3 | ||||||||
| G6 – 45c | 1396 | 1528 | 5 | 0.19 | 0.73 | 1.41-1.58 | III-5 | |||||||||
| G6 – 27c | 1414 | 1544 | 0 | 0.20 | 0.66 | |||||||||||
| A6♭ – 40c | 1501 | 1623 | 4 | 0.18 | 0.52 | 0.88 | 1.51-1.58 | IV-4 | ||||||||
| A6♭ – 36c | 1505 | 1627 | 0 | 0.90 | 0.20 | |||||||||||
| A6♭ + 27c | 1568 | 1687 | 0 | 0.58 | 1.32 | |||||||||||
| A6 – 42c | 1599 | 1718 | 0 | 0.18 | 0.39 | 0.88 | 1.36 | |||||||||
| A6 + 7c | 1648 | 1767 | 6 | 0.23 | 1.39-1.58 | II-6 | ||||||||||
| 4th from double octave | B6♭ + 1c | 1742 | 1866 | 7 | 0.90 | 1.58 | I-7 | |||||||||
| B6 – 22c | 1819 | 1951 | 5 | 0.19 | 0.50 | 0.91 | 1.37-1.58 | IV-5 | ||||||||
| B6 – 19c | 1822 | 1954 | 1 | 0.18 | 0.39 | 0.71 | 1.07 | 1.49 | ||||||||
| B6 + 39c | 1880 | 2021 | 6 | 0.21 | 0.70 | 1.37-1.58 | III-6 | |||||||||
| B6 + 45c | 1886 | 2028 | 2 | 0.17 | 0.35 | 0.74 | 1.07 | 1.50-1.58 | V-2 | |||||||
| C7 + 30c | 1971 | 2130 | 3 | 0.17 | 0.46 | 0.71 | 1.04 | 1.46-1.58 | V-3 | |||||||
| C7# + 21c | 2062 | 2244 | 4 | 0.17 | 0.39 | 0.71 | 1.05 | 1.46-1.58 | V-4 | |||||||
| C7# + 42c | 2083 | 2272 | 7 | 0.20 | 1.18-1.58 | II-7 | ||||||||||
| 6th from double octave | D7 – 14c | 2127 | 2330 | 8 | 0.65 | 1.58 | I-8 | |||||||||
| D7 + 0c | 2141 | 2349 | 1 | 0.14 | 0.38 | 0.62 | 0.92 | 1.19 | 1.50 | |||||||
| D7 + 32c | 2173 | 2393 | 6 | 0.16 | 0.48 | 0.91 | 1.37-1.58 | IV-6 | ||||||||
| D7 + 48c | 2189 | 2415 | 2 | 0.22 | 0.66 | 0.88 | 1.18 | 1.46 | 1.58 | VI-2 | ||||||
| D7# – 49c | 2192 | 2420 | 3 | 0.22 | 0.64 | 0.89 | 1.18 | 1.46 | 1.58 | VI-3 | ||||||
| D7# + 2c | 2243 | 2492 | 5 | 0.41 | 0.73 | 1.04 | 1.45-1.58 | 1.46 | 1.58 | V-5 | ||||||
| D7# + 30c | 2271 | 2532 | 4 | 0.16 | 0.39 | 0.73 | 1.05 | 1.37 | 1.55-1.58 | VI-4 | ||||||
| E7 – 41c | 2300 | 2575 | 7 | 0.19 | 0.66 | 1.41-1.58 | III-7 | |||||||||
Table I. The tone analysis of an arbitrary F4 bell. The place striking on the outside wall is at H / R0 = 0.16, where R0 = 0.58m.
Table I shows the results of measurements on a bell with a hum note 43 cents below F3 ( 170.3 Hz). The first column shows the name of each mode, and the second column shows the measured mode frequency in musical notation, which includes the note name and the interval (in cents) to the nominal. The third column lists the frequencies of the partials. The fourth column gives the number of nodal meridians (s). Because of the rotational symmetry of a bell, the number of meridians is sufficient. This notation is different from the conventional one in campanology, where the number of nodal lines are counted when showing any given parallel along the outline of the bell. When considering the bell as a curved plate, as Rayleigh did, the plate notation can also be used for the bell. Thus the hum note, for instance, is described here by two (s = 2) instead of by four meridians, as every nodal meridian goes through the head of the bell and continues on the other side with an azimuth difference of 180°. One can imagine that, for pure bending modes, a minimum of four half-meridians (s = 2) is required. Behavior of partials corresponding to s values of 0 and 1 represents extensional vibrations, discussed in the next section.
The fifth column gives the position of nodal circles on the outside surface of the bell measured from the base. The use of cylindrical coordinates is most convenient here, with R being the radius measured from the center line, H the height above the base, and φ the azimuth on the wall measured from an arbitrary reference point. The azimuth angle will be important only when the bell has an asymmetry in the outline (e.g., irregularities in the bell bronze), causing a dependence on the position of nodal meridians. Position of nodal circles can be recorded properly only when the bell model is known. Since there is a great variety of models, and since the bell profile can hardly be represented by a mathematical formula (Rayleigh, 1890; Vas Nunes, 1909), one has to mention at least some characteristic features of the profile. First of all, the position of nodal lines for the various modes is considered. But that alone is not sufficient, as it does not say anything about the model having a thick or a thin wall. The latter, however, can be expressed by the constant k in terms of R0 and the hum-note frequency. As two bells can have the same hum note, and the dependence of upper partials on the model is not known yet, it is also useful to introduce the constant c/k (see also Sec. III). This constant provides information about the finer details of the model. Finally, the height of the bell expressed as H0 / R0 is an important parameter. Thus it is useful to measure the height HO of the bell along the main axis from the base to the center of the head. This value is important because longer bells need a greater mass concentration in the head. Relevant characteristics for the bell considered here are: k = 97.4m/s; c/k = 47.0 kg s/m4; H0 / R0 = 1.57. These characteristics, together with the other measurements, enable reasonable comparison with other bell models.
Flexural vibrations tend to confine their motions to the sound bow and the lower part of the waist. Especially partials having nodes in the waist and the head show this tendency. For some of these, no vibration could be measured in the region from the nodal circle in the waist to the head, which is reflected in Table I by either a question mark or a set of two numbers indicating an uncertainty range. Most flexural vibrations have no sharply defined node in the head either. Since amplitudes are very small there, a precise node is difficult to locate and is subject to considerable experimental error.
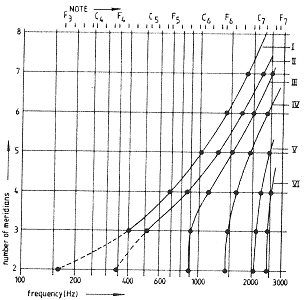
FIG. 2. Group division of the partials of the F4 bell shown in Table I. Each group contains partials with the same number of nodal circles in the same position on the bell surface, with increasing number of meridians.
Figure 2 shows a division of flexural vibrations into groups. These groups, wherever appropriate, are also shown in the sixth column of Table I. When the lower two partials (hum note and fundamental) are temporarily disregarded, the following groups appear:
Group I. Partials of this group have a circular node in the waist and in the head.
Group II. These partials have a node in the head and also one in the sound bow of the bell. The number of nodal circles is thus the same as for the first group, but the position on the bell’s surface is quite different. That is the reason why position of the parallel node is an important parameter in defining a group.
Group III. This group has three nodal circles, one in the head, one in the waist, and one in the sound bow. The lowest partial of this group corresponds to s = 2, so this is the first complete group of bell partials.
Group IV and higher. Each group has one nodal circle more than the one before. All these groups are complete, i.e., their lowest partials correspond to a meridian pattern of s = 2.
The lowest partials of groups I and II, those corresponding to the meridian patterns = 2, appear to be absent. Of the two temporarily disregarded frequencies, the hum note has no node in the waist, and the second partial (fundamental) has one halfway between sound bow and waist. When hum note and fundamental cannot be classified, one might wonder which properties of the bell cause them. A bell does not exactly behave as simpler modelled bodies such as conical, spherical, or cylindrical shells. It is true that also here the hum note has no node in the waist, but in these cases it is not the only such mode. On the other hand, we do not know of shells having partials with only a node in the waist and head, so that the first group seems very bell-like in its properties. The hum note can always serve as the lowest of a group of tones with nodes only in the head. Moreover, one will never find two groups of partials that differ only in the position of their nodal circles, as do the first and second group of a bell. So it may be fair to assume that the hum note of a bell represents the first tone of the first group, where, because of the particular character of the bell shape, the higher tones of this group have an extra node in the waist. Similar reasons justify viewing the fundamental as the first member of the second group. This classification remains mostly hypothetical, however, until it is supported by further empirical evidence. The uncertainty on this point is shown in Fig. 2 by the dotted lines.
II. Extensional Vibrations
Extensional vibrations are oscillations in which the restoring force does not result from wall bending, as it is in transverse or flexural modes, but from (longitudinal) stretching along the body wall. The lowest extensional mode of a ring is also one in which it alternately expands and contracts concentrically. The fact that a bell may have extensional modes was already noted by Jones and Alderman (1933) . Their frequencies are normally high, as can be expected from the very large restoring forces that go with such modes.
| Name | Note | Frequency (Hz) |
|---|---|---|
| Hum note | E4 – 46c | 321 |
| Fundamental | D5 – 70c | 564 |
| I-3 | G5 – 46c | 763 |
| II-3 | B5 – 61c | 964 |
| Ext. vibr. (s = 1; m = 2) | E6♭ – 9c | 1238 |
| I-4 | E6 – 42c | 1287 |
| III-2 | F6# – 4c | 1477 |
| III-3 | F6# + 28c | 1504 |
| Ext. vibr. (s = 0; m = 2) | G6 + 17c | 1583 |
| II-4 | G6# – 1c | 1661 |
| Ext. vibr. (s = 0; m = 1) | A6 – 4c | 1756 |
| I-4 | B6 – 20c | 1946 |
| III-4 | B6 + 44c | 2026 |
| Ext. vibr. (s = 0; m = 4) | D7 – 3c | 2345 |
| IV-3 | D7 + 31c | 2392 |
| I-6 | E7 + 36c | 2692 |
Table II. The tone analysis of a bell by Thomas Both, 1591, in which an extensional vibration occurs below the nominal I-4. The number of circular nodes is given by ,. Some constants characterizing this bell are: k = 106.9 m/s; c/k = 55.0 kg s/m; H0 / R0 = 1.70: R0 = 0.34m.
Certain circumstances can arise, however, where an extensional vibration occurs below the nominal I-4. An example is the bell by Thomas Both, whose tone analysis is given in Table II. This bell appears to have an extensional vibration, about a semitone under the nominal I-4, with one nodal meridian and two nodal circles, one lying a little above the sound bow and the other lying slightly below the head of the bell. This partial can be heard through the beats it produces with the nominal. It is not difficult to explain the position of this mode in the sound spectrum. This bell differs from normal, especially in height. The value of H0 / R0, which usually is about 1.60, is here 1.71, causing the fundamental (70 cents below D5) to be much too low with respect to the first group. Because the shape is completely different compared to a good octave bell, the tuning has totally altered also. Thus one should expect that extensional vibration frequencies have a very different position in the tonal spectrum also. A precise explanation of the low extensional mode frequency in this case is, of course, much more difficult.
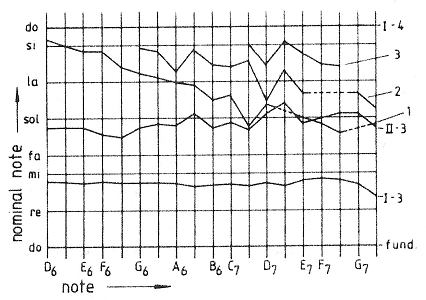
FIG. 3. Three extensional mode frequencies (1, 2, 3) in relation to some flexural mode frequencies (I-3, I-4, II-3) in a series of experimental carillon bells. Notice the decreasing relative spectral position of extensional mode frequencies with increasing strike note or wall thickness. The lower “do” on the ordinate is an arbitrary reference, taken at the strike note.
Ringing bells with extensional mode frequencies in spectral regions that establish the purity of a bell are rarely found. This is different, however, with carillon bells. Figure 3 shows mode frequencies for a series of experimental carillon bells. Several mode frequencies are plotted as a function of the “nominal pitch” (strike note) of each bell, where frequencies of comparable modes have been connected for visual convenience.
In studying this graph, one notices first of all that the thirds (I-3) are almost all tuned sharp. This represents a compromise, first proposed by van Geyseghem (1935), that is aimed at making the carillon better suited for playing music in both major and minor keys. There is doubt, however, whether such bells with a “neutral” third, which is about halfway between a minor and a major third, can be wholly satisfactory because of their lack of harmonic coherence (Lehr, 1956). The fifths (II-3) of these bells are generally not very pure either. Hardly any attention was paid to the fifths when tuning these bells, because the purpose of the experiment was to produce bells with a larger third.
The base chord, comprising flexural vibrations only, has generally been maintained throughout the series of bells. In contrast to these partials, there are some modes that successively turn up below the nominal in the D6, G6, and C#7 bells. Characteristic for these partials is their increasing difference compared to the frequency of the nominal I-4 with increasing strike note. Apparently these partials do not follow the normal laws for tuning the first five flexural partials, suggesting that they might be extensional modes. This was shown directly when displacement functions of these tones were investigated. The first extensional partial has one meridian node and two nodal circles at H / R0 = 0.25 and H / R0 = 0.75. The second has no nodal meridians, and no clear picture could be obtained about the nodal circles since in the waist, from H / R0 = 0.20 to H / R0 = 1.45, the wall hardly vibrated at this extensional partial. Finally, the third extensional partial again has one meridian and one nodal circle at H / R0 = 0.20.
To interpret the difference in properties between extensional and flexural vibrations, one only needs to remember that in carillon bells the value of k increases with increasing picch of the strike note, which means that the wall becomes relatively thicker. That explains why the frequency of these extensional partials becomes relatively lower. From a simple theoretical viewpoint, the frequencies of extensional vibrations in a cylindrical, conical, or spherical shell depend only on diameter and height, and not on wall thickness.
Precise values for the carillon bells shown in Fig. 3 are given in Table III. The tuning of relevant partials for each bell is given in column 4, where given successively are: hum note; fundamental; third 1-3; fifth 11-3; the first, second, and third extensional partials relative to the frequency of the nominal; and finally the nominal 1-4. In other columns, some calculated characteristic values of each bell are given such as c, k and c/k for the hum note and the first two extensional partials. Furthermore, the value of H0 / R0 is given for each bell. Also included at the top of Table III are some larger bells which do not show extensional partials below the frequency of the nominal. They are separated from the others by a dividing line.
| Deviations in cents | Frequencies (Hz) | k = f R0 (m/s) | c | c/k (kg s/m4) | H0/R0 | ||||||||||||||||
| Note | R0(m) | M(kg) | h.n. | fund | I-3 | II-3 | 1 | 2 | 3 | I-4 | h.n | 1 | 2 | h.n | 1 | 2 | (kg/m3) | h.n | 1 | 2 | |
| C5 | 0.385 | 266 | 0 | 0 | 32 | 6 | 125 | 46 | -1 | 261.6 | 1125 | 1075 | 100.7 | 433.1 | 413.9 | 4661 | 46.3 | 10.8 | 11.3 | 1.63 | |
| F5# | 0.282 | 112 | -1 | -2 | 36 | 14 | 90 | 33 | -1 | 369.8 | 1559 | 1509 | 104.3 | 439.6 | 425.5 | 4994 | 47.8 | 11.4 | 11.7 | 1.63 | |
| G5 | 0.271 | 99 | -1 | 1 | 27 | 16 | 55 | 80 | -1 | 391.8 | 1619 | 1642 | 106.2 | 438.7 | 445.0 | 4974 | 46.7 | 11.3 | 11.1 | 1.63 | |
| A5# | 0.232 | 70 | 0 | -1 | 22 | -13 | 15 | 112 | 1 | 466.2 | 1881 | 1989 | 108.2 | 436.4 | 461.4 | 5606 | 51.8 | 12.9 | 12.2 | 1.63 | |
| B5 | 0.225 | 63 | 1 | 2 | 18 | 9 | 5 | 158 | 0 | 494.2 | 1981 | 2164 | 111.2 | 445.7 | 486.9 | 5531 | 49.6 | 12.4 | 11.4 | 1.63 | |
| D6 | 0.200 | 47 | 2 | -2 | 56 | -56 | -70 | -2 | 588.0 | 2256 | 117.6 | 451.2 | 5875 | 49.8 | 13.0 | 1.62 | |||||
| D6# | 0.191 | 42 | 1 | 0 | 52 | -53 | -103 | -4 | 622.6 | 2345 | 118.9 | 447.9 | 6028 | 50.7 | 13.5 | 1.62 | |||||
| E6 | 0.185 | 41 | -1 | 1 | 46 | -53 | -123 | 0 | 658.9 | 2456 | 121.9 | 454.4 | 6475 | 53.0 | 14.3 | 1.61 | |||||
| F6 | 0.180 | 35 | -3 | -2 | 56 | -88 | -128 | -2 | 697.3 | 2595 | 125.5 | 467.1 | 6002 | 47.8 | 12.8 | 1.61 | |||||
| F6# | 0.171 | 32 | -1 | -1 | 48 | -100 | -220 | 0 | 739.6 | 2607 | 126.5 | 445.8 | 6400 | 50.6 | 14.4 | 1.60 | |||||
| G6 | 0.167 | 31 | 0 | 0 | 41 | -55 | -258 | -118 | 0 | 784.0 | 2702 | 2929 | 130.9 | 451.2 | 489.2 | 6656 | 50.8 | 14.7 | 13.6 | 1.59 | |
| G6# | 0.161 | 28 | -1 | -1 | 42 | -36 | -282 | -136 | 0 | 830.1 | 2823 | 3071 | 133.6 | 454.4 | 494.4 | 6719 | 50.3 | 14.8 | 13.6 | 1.58 | |
| A6 | 0.155 | 25 | -2 | -2 | 40 | -38 | -308 | -258 | 2 | 879.0 | 2946 | 3033 | 136.2 | 456.3 | 470.1 | 6714 | 49.3 | 14.7 | 14.3 | 1.57 | |
| A6# | 0.153 | 26 | -1 | -3 | 29 | 22 | -322 | -134 | 3 | 931.8 | 3096 | 3452 | 142.6 | 473.7 | 528.2 | 7259 | 50.9 | 15.3 | 13.7 | 1.56 | |
| B6 | 0.144 | 24 | -1 | 0 | 34 | -57 | -402 | -219 | 1 | 987.2 | 3132 | 3482 | 142.2 | 451.0 | 501.4 | 8038 | 56.5 | 17.8 | 16.0 | 1.55 | |
| C7 | 0.140 | 20 | 0 | -3 | 36 | -23 | -386 | -224 | 0 | 1046.5 | 3349 | 3678 | 146.5 | 468.9 | 514.9 | 7289 | 49.8 | 15.5 | 14.2 | 1.54 | |
| C7# | 0.134 | 18 | 0 | 0 | 26 | -60 | -547 | -196 | -92 | 2 | 1108.7 | 3234 | 3960 | 148.6 | 433.4 | 530.6 | 7481 | 50.4 | 17.3 | 14.1 | 1.53 |
| D7 | 0.132 | 18 | 0 | 0 | 40 | 6 | -420 | -408 | -209 | 0 | 1174.7 | 3687 | 3712 | 155.1 | 486.7 | 490.0 | 7826 | 50.5 | 16.1 | 16.0 | 1.52 |
| D7# | 0.127 | 18 | -2 | 0 | 24 | 80 | ? | -232 | -87 | 0 | 1243.1 | ? | 4354 | 157.9 | ? | 553.0 | 8788 | 55.6 | ? | 15.9 | 1.51 |
| E7 | 0.126 | 17 | 0 | 0 | 54 | -32 | -501 | -367 | -143 | 0 | 1318.5 | 3949 | 4267 | 166.1 | 497.6 | 537.6 | 8498 | 51.2 | 17.1 | 15.8 | 1.50 |
| F7 | 0.123 | 15 | 2 | 2 | 63 | -23 | -528 | ? | -210 | 3 | 1398.5 | 4119 | ? | 172.0 | 506.6 | ? | 7523 | 43.8 | 14.9 | ? | 1.49 |
| F7# | 0.117 | 14 | -2 | 0 | 58 | 4 | -580 | ? | -220 | 2 | 1478.3 | 4235 | ? | 173.0 | 495.5 | ? | 6943 | 40.2 | 14.0 | ? | 1.48 |
| G7 | 0.117 | 15 | 0 | 3 | 34 | 21 | ? | -370 | 1568.0 | ? | 5065 | 183.5 | ? | 592.6 | 7439 | 40.5 | ? | 12.6 | 1.47 | ||
| G7# | 0.116 | 15 | 3 | 4 | -38 | -57 | -537 | -448 | 1664.1 | 4873 | 5130 | 193.0 | 565.3 | 595.1 | 9610 | 49.8 | 17.0 | 16.1 | 1.46 | ||
Table III. The tone analysis of various experimental carillon bells sketched in Fig. 3. For the flexural partials, deviations from their respective equal tempered values are given in cents. For the extensional partials, deviations are measured from the correct value of the nominal I-4.
Inspection of Table III shows that the magnitude of c/k remains almost constant for the hum note, and therefore for all the tuned flexural partials. This is not true for the extensional partials which show a distinct increase for the value c/k with increasing strike note. This once more demonstrates the extensional character of these overtones. Somewhat inconsistent with this notion, however, is the fact that the frequencies of these partials show a small rise. This suggests that these tones are perhaps an intermediate form of extensional and flexural modes. The fact that frequencies of these partials depend on small changes in the bell profile supports this idea. When the pitch of the stike note of carillon bells is increased, not only is the wall made thicker, but the profile is also altered a little, insignificant as this change may be compared with the change in wall thickness. The possibility therefore remains that, in practice, the extensional partials are independent of wall thickness. More about this will be said in the next section.
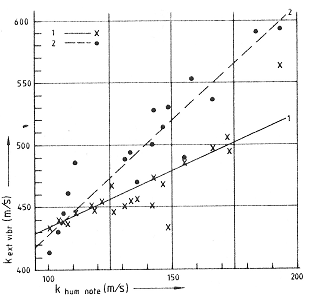
FIG. 4. The k values of two extensional modes as a function of the k value of the hum note, taken from data shown in Table III, demonstrating that extensional vibrations differ essentially from flexural vibrations.
In Fig. 4, k values for the first two extensional vibrations are compared with those of the hum note. Despite the large spread in the data points, a point can certainly be found where the order of the first and second extensional partials changes, so it may be expected that in a normal ringing bell both extensional partials occur in the order two-one, which actually does happen in practice.
Finally, one should remember that all extensional partials have an antinode in the head of the bell, so the intensities of these tones should be strongly muted when the bell is suspended. Indeed, this was found to be the case. This suggests that extensional partials are generally of only secondary importance in forming the tone of a bell. Sometimes, however, they can have an audibly disturbing effect, e.g., when an extensional vibration and the nominal I-4 almost coincide. The beats that are created will make the bell lose its pure tone, as has been observed in practice.
III. Variations in Wall Thickness
Wall thickness of carillon bells increases with increasing strike note. Because of this increasing thickness, one can no longer talk about a series of similar profiles. Therefore, it is important to know how this affects the partial frequencies. A simple theoretical starting point is to assume that, in accordance with elementary theory, frequencies of flexural modes vary linearly with wall thickness and frequencies of extensional modes are insensitive to wall thickness changes. When making the bells heavier, both types of modes will shift with respect to each other, gradually changing the pattern of the original tone spectrum.
Earlier statistical investigations showed that lower partials may be considered as flexural vibrations in accordance with elementary theory (Lehr, 1952). This is expressed by the fact that the ratio c/k remains constant for a series of bells that differ only in wall thickness. Combination of Eqs. (1) and (2) yields:
(3) M = (c/k)fR04
With the aid of Eq. (3) it is easily verified that a constant ratio c/k implies a linear dependence of frequency on wall thickness. Since M is proportional to DR03, in which D represents the wall thickness, Eq. (3) can be written as
(4) f = c’D/R02
in which c’ is a constant that depends only on the profile and is different for every flexural partial. Equation (4) expresses one of the primary properties of vibration in elementary bending theory. Care must be taken, however, when interpreting the remaining constant c/k in the light of normal practice of bell casting. In carillon bells, not only is the wall thickened, but the profiles are altered as well. This is done because the base chord will remain within tolerable limits only if there is no wall thickening, or at the most, a very slight one. When greater wall thickenings are applied, it is inevitable that the base chord becomes considerably altered. Since a first requirement of carillon bells is that the bells have the same base chord, corrections must be made. This is achieved by altering the profiles at definite places, e.g., the sound bow may be placed higher or the height of the bell may be decreased. This can be seen in Table III as the gradual decrease of the value of H0 / R0 from 1.65 to 1.46. These observations could lead to the practical observation that the dependence of partial frequencies on wall thickness, besides being different for every overtone, is not completely linear.
Despite alterations and corrections in the standard profile, the ratio c/k remains constant for the tuned flexural partials, provided that corrections have been made properly. All base chords should remain the same, a fact that can be observed in the bells of Table III. We therefore cannot draw any general conclusions from the fact that the ratio c/k is constant in existing carillons. Generally, therefore, Eq. (4) is better written as
(5) f = c’Da / (R0a + 1)
The exponent provides information about the character of the overtone in question. Its numerical value, which is always less than one, depends on the profile and on the vibration mode. Linear dependence of flexural mode frequency on wall thickness holds, according to elementary bending theory, only when the thickness is many times smaller than the main dimensions of the body in question, in this case R0. Figure I shows that this condition is by no means satisfied in a typical bell. As for a thick bar, the bell model will need some corrections that include rotation energy and deformation of the longitudinal section of each element caused by shear forces. Such a model will show systema1ic deviation from linear behavior between frequency and wall thickness. One may wonder whether the type of function shown in Eq. (5) can give a reasonable description of observed behavior of bells that differ only in wall thickness.
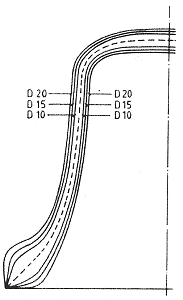
FIG. 5. Profiles of experimental D bells used to investigate dependence of partial frequencies on wall thickness. R0 = 0.25m.
To find out, three such bells were cast. A sketch of the models is given in Fig. 5. An arbitrary model was taken as base profile (DIO). Since a pure physical experiment was involved here, no attention was paid to tuning the bell. A particular problem with the derivation of other bells of different thickness from this one base profile is the definition of a middle surface, which is essential in the determination of the thickness at certain parts on the bell surface such as, e.g., the sound bow where inside and outside surface are not at all parallel. In simple structures the middle surface is, according to elementary bending theory, a neutral layer in which no tension or compression forces occur. Bells, however, are by no means simple structures, and one should therefore not assume that the middle surface is also the neutral layer. The Rayleigh method of de1ermining thickness as the points of intersection of the perpendicular through the middle surface with the wall surfaces is therefore not necessarily the proper one. As long as no better theoretical insight in the internal forces in the bell is available, however, it seems reasonable for the purpose of this experiment to use the middle surface as reference for determining the precise location of inside and outside walls for the derived bells.
Two other bells were cast, one 1.5 times as thick as the base model (D15), and one 1.97 times as thick (D20). The natural frequencies of these bells are shown in Table IV.
TABLE IV. The tone analysis of the three D-bells and values of the parameter a which indicates dependence of partial frequencies on wall thickness, according to equations (5) and (6).
| D10 | D15 | D20 | a | a | a | |||||
| Partial | Note | f(Hz) | Note | f(Hz) | Note | f(Hz) | D15/D10 | D20/D10 | avg. | |
| Hum note | G4 – 30 | 385 | C5 – 47 | 509 | D5# + 9 | 626 | 0.695 | 0.717 | 0.71 | |
| Fund. | G5 – 69 | 753 | A5 + 50 | 906 | C6 + 9 | 1052 | 0.470 | 0.493 | 0.48 | |
| I-3 | A5# + 17 | 942 | D6# – 10 | 1237 | G6 – 48 | 1525 | 0.672 | 0.710 | 0.69 | |
| II-3 | C6# – 53 | 1075 | G6 – 59 | 1515 | A6# + 42 | 1910 | 0.846 | 0.848 | 0.85 | |
| I-4 | G6 – 4 | 1564 | C7 + 17 | 2114 | E7 – 17 | 2611 | 0.744 | 0.756 | 0.75 | |
| II-4 | A6# – 62 | 1799 | D7# + 49 | 2561 | G7# – 64 | 3202 | 0.870 | 0.850 | 0.86 | |
| III-3 | A6# – 2 | 1863 | D7# – 31 | 2445 | F7# – 29 | 2911 | 0.672 | 0.659 | 0.66 | |
| III-2 | A6# + 25 | 1892 | C7# – 34 | 2174 | D7 + 40 | 2404 | 0.342 | 0.354 | 0.35 | |
| I-5 | D7 + 1 | 2351 | G7 + 11 | 3156 | A7# + 61 | 3863 | 0.726 | 0.732 | 0.73 | |
| III-4 | D7 + 16 | 2371 | G7# – 19 | 3286 | B7 + 25 | 4009 | 0.805 | 0.775 | 0.79 | |
| II-5 | E7 + 4 | 2643 | A7# + 30 | 3817 | D8 – 4 | 4687 | 0.906 | 0.844 | 0.86 | |
| IV-2 | F7# + 2 | 2963 | G7# + 29 | 3379 | C8 – 31 | 4112 | 0.325 | 0.484 | 0.40 | |
| IV-3 | F7# + 22 | 2998 | A7# + 5 | 3740 | C8# – 51 | 4306 | 0.544 | 0.534 | 0.54 | |
| III-3 | G7 + 27 | 3185 | C8# + 13 | 4468 | F8 + 41 | 5722 | 0.836 | 0.864 | 0.85 | |
| I-6 | G7 + 68 | 3262 | C8# – 46 | 4319 | E8 – 26 | 5195 | 0.692 | 0.686 | 0.69 | |
| Extensional vibrations | ||||||||||
| s = 1 | m = 2 | G6# – 30 | 1633 | A6 – 52 | 1708 | A6 – 33 | 1727 | 0.011 | 0.008 | 0.01 |
| s = 1 | m = 2 | B6 – 45 | 1925 | B6 – 30 | 1942 | B6 – 10 | 1964 | 0.002 | 0.003 | 0.00 |
| s = 0 | m = 2 | B6 – 10 | 1964 | B6 – 12 | 1962 | B6 – 8 | 1966 | -0.002 | 0.001 | 0.00 |
| s = 1 | m = 1 | C7# – 10 | 2205 | C7# + 11 | 2232 | C7# + 30 | 2256 | 0.003 | 0.003 | 0.00 |
| s = 1 | m = 3 | F7 – 10 | 2778 | F7 + 40 | 2859 | F7# + 26 | 3005 | 0.007 | 0.011 | 0.01 |
TABLE IV. The tone analysis of the three D-bells and values of the parameter a which indicates dependence of partial frequencies on wall thickness, according to equations (5) and (6).
The upper part shows the flexural mode frequencies, whose order deserves some comment. One sees that the base profile D10 has rather impure tone relations. For instance, the fifth II-3 and the decime II-4 are both about half a tone too low, and the fundamental is also on the low side. Similarly, the undecimes III-2 and III-3 are one tone too low. Apparently the intervals between partials of the same group are almost maintained in this model, while entire groups have been shifted in frequency with respect to one another. Such phenomena are almost always found in an impure bell. One rarely finds a bell, for instance, whose interval between the fifth II-3 and the decime II-4 is not a sixth.
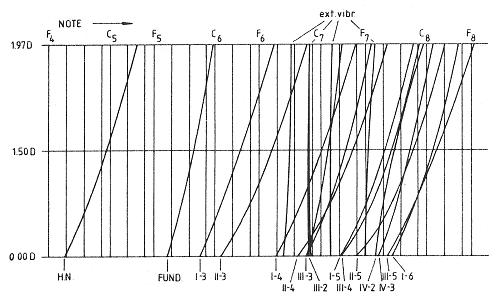
FIG. 6. Some flexural and extensional mode frequencies of the three D bells shown on the ordinate. The abscissa represents partial frequency in musical notation. Each function is an interpolation from three point values. Characteristic dimensions are: for D10, k = 99.3 m/s; c/k = 43.0 kg s/m4; for D15, k = 131.3 m/s; c/k = 48.8 kg s/m4; for D20; k = 161.4 m/s; c/k = 53.9 kg s/m4. For all bells, H0/R0 = 1.56; R0 = 0.25m.
The lower part of Table IV shows the extensional partials. Both types of partials are also plotted out in Fig. 6, where points that represent frequencies of comparable modes of the three bells have been connected for visual convenience. From this figure one sees that, going from D10 to D20, the frequencies of the first group (I-x) all rise by the same interval. The same happens to the tones of the second group (II-x), although they rise more than those of the first group. Hence it seems that partials of one group depend similarly on wall thickness and profile, whereas partials from different groups show a different dependence. Thus it can happen that two tones can be mistaken for one another, especially in the mixture range of the bell where intervals between partials are generally small. One sometimes finds bells in which both the undecimes III-2 and III-3 are lower than the decime II-4, which also holds for DI5 and D20. Figure 6 also shows quite clearly that the double octave I-6 is not uniquely defined as a tone “about an interval of an octave above the nominal,” since many more tones would qualify for that consideration. This underscores the need for physical qualifiers besides the usual musical ones. Bell partials should not be named merely on the basis of their frequencies but also on the basis of their physical mode properties. For example, the “double octave” mode is not merely that mode whose frequency comes closest to twice the frequency of the “nominal” or four times that of the ” fundamental.” It must also correspond to the mode pattern I-6 and be sufficiently intense to be heard.
The tones shown in Table IV can be accounted for by Eq. (5). To calculate the exponent, one must convert Eq. (5) to a relative expression. In Eq. (5). the thickness D appears without specification as to where on the bell surface this thickness is measured. It is therefore more convenient to take bell D10 as reference and to take its magnitudes as unity. When the frequency of a partial, the thickness, and the radius of this reference bell are fc, Dc and Rc respectively, one can show that for every other profile with the same radius R, (such as D15 and D20) the following relation holds:
(6) f/fc = (D/Dc)a, or i = da,
where i represents the ratio of partial frequency increase resulting from increasing wall thickness by a factor d. Table IV gives values of a, computed be1ween D10 and D15, and between D10 and D20. The last column gives the average of these two values. For the hum note and the modes group I, the average value of a approximately equals 1/root2; for the fundamental and the modes of group IV, the average value of a is close to 1/2.
Extensional vibrations appear to follow theoretical behavior exactly, i.e., their frequencies do not depend on wall thickness. Behavior of flexural modes is different, however, as the value of a varies between 0.35 and 0.86. Coherence of mode groups is also more or less established here. For the first group, the value of a is the same as for the hum note (0.71), while for the second group this is 0.86. This supports the suggestion made earlier to classify the hum note as the lowest member of the first group (I-2). The value of a found for the fundamental, however, is considerably lower than that of the second group, which does not support the idea of viewing the fundamental as the lowest partial in the second group (II-2). Values of a in the third group showed too much of a spread to justify computation of an average. Partials having two meridian nodes (I-2, III-2, IV-2) seem to rise less in frequency with increasing wall thickness compared with other tones in the group they belong to. An exception is the hum note (I-2), given that it is correct to consider it a member of the first group.
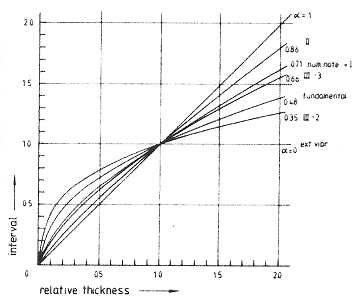
FIG. 7. Relative frequency as a function of relative thickness for several partials, according to Eq. (6). Within groups, there is some similarity in sensitivity to wall thickness.
The various values of a are, with the aid of Eq. (6), graphically represented in Fig. 7. Only the most important partials are shown. Extrapolations were made for d values less than unity. This part of the graph must be interpreted with caution, since it represents no empirical data points. Comparison of this figure with graphs for vibrations of a ring calculated by Federhofer (1950) suggests that it may be possible to account for bell vibrations with an extensive theory of bending vibrations. The high value of a for the second group of partials can, for instance, be explained by the fact that these partials mostly vibrate in the waist, where the bell nearly acts as a cylinder. They are relatively less dependent on the thick sound bow because of the node at that place. This suggests that these modes may be more easily calculated than partials of the first group.
IV. Musical Consequences
Inspection of Table I shows that there is quite a difference between ideal partial intervals, indicated by their musical names and shown in the first column, and their actual values shown m the second column. Whether these differences are important or not depends on the intensity of the partials. As partials of group I all have a node in the waist, they are expected to dominate the total bell sound because the clapper always strikes the sound bow. This involves the partials I-3 (minor third), 1-4 (nominal), 1-5 (duodecime), 1-6 (double octave), etc., which are found in most bells (Slaymaker and Meeker, 1954). That is why so much attention is paid to these partials when tuning a bell. The fifth (II-3) and the decime (II-4) bo1h have a node slightly above the sound bow, so they will be much weaker. That is why little attention is paid to these partials during tuning, although care should be taken that deviations are not too large. Too flat a fifth results in an uncongenial character of the bell. Also, the fact that the major decime (II-4) is not a minor decime (regardless of the question of whether this would be possible without disturbing other important tonal relations), is perhaps tolerable only because the partial is not very strong. There are bells that have a minor decime (II-4), but inspection of such bells shows invariably that this interval is accompanied by a flattened fifth (II-3). This is consistent with our earlier observation that intervals are maintained within one group and that only whole groups can be shifted mutually.
The higher modes of the second group and modes of higher-order groups are apparently perceptually so insignificant that no one until now has paid much attention to their position in the sound spectrum. From a musical point of view it might seem undesirable that the minor third (I-3) occurs together with a major decime (II-4), or that there are two undecimes (III-2 and III-3) which are about 30 cents different from each 01her, while neither one fits in the musical pattern. The point, however, is that all these modes have a nodal ring near the sound bow, so they will, because of their relative weakness, at most be able to affect the timbre of the bell, as the fifth (II-3) and the decime (II-4) do. Thus it is desirable to select the striking point of the clapper in such a way that these tones will not disturb the bell’s timbre, which is based mostly on partials of the first group.
The bell sound that the listener hears consists mainly of strong flexural vibrations. The motions of extensional vibrations are greatly limited by the suspension of the bell. These tones will radiate only weakly from the sound bow and are of only minor importance. From a musical viewpoint this means that extensional vibrations may influence only the timbre of the bell but not the purity of tuning, which is a property they have in common with all high partials.
Because of the apparent group structure of bell partials, one may expect that intervals of partials within a group always follow certain rules. For example, when the nominal (I-4) is too low with respect to the third (I-3), one expects the entire first group to have a more compact chord structure. This has significant musical consequences. It is well known that in most bells the frequency of the double octave (I-6) is not quite correct. If one attempts to tune it exactly one octave above the nominal (I-4), the other tones are altered as well. Tone frequencies of bells by various founders, shown in Table V, illustrate this fact.
| Founder and year of casting | Ideal bell | Eijsbouts 1954 | Eijsbouts 1955 | Eijsbouts 1955 | Bourlet 1679 | vd Ghein 1615 | Unknown 1905 |
|---|---|---|---|---|---|---|---|
| k (m/s) | … | 98.8 | 99.4 | 101.1 | 99.2 | 98.3 | 96.9 |
| c/k (kg s/m4) | … | 49.0 | 46.9 | 48.1 | 41.6 | 40.2 | 46.1 |
| H0/R0 | … | 1.57 | 1.57 | 1.57 | 1.50 | 1.59 | 1.82 |
| Strike note | … | E4♭ – 23 | G4# – 20 | B4♭ + 40 | F4 – 11 | C5 + 16 | B4♭ – 11 |
| f (strike note) | … | 307.0 | 410.5 | 477.1 | 367.7 | 528.1 | 463.2 |
| Partial | Ratio to the strike note | ||||||
| Hum note | C3 0.50 | 0.50 | 0.50 | 0.49 | 0.50 | 0.50 | 0.50 |
| Fundamental | C4 1.00 | 1.00 | 1.00 | 1.02 | 1.01 | 1.02 | 0.92 |
| I-3 tierce | E4♭ 1.20 | 1.20 | 1.20 | 1.18 | 1.28 | 1.20 | 1.19 |
| II-3 quint | G4 1.50 | 1.50 | 1.50 | 1.48 | 1.55 | 1.42 | 1.44 |
| I-4 nominal | C5 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| II-4 | E5 2.50 | 2.57 | 2.62 | 2.56 | 2.57 | 2.15 | 2.26 |
| I-5 superquint | G5 3.00 | 3.00 | 2.99 | 2.96 | 3.01 | 3.15 | 3.01 |
| I-6 octave nominal | C6 4.00 | 4.14 | 4.15 | 4.10 | 4.13 | 4.37 | 4.05 |
| I-7 | F6 5.33 | 5.42 | 5.40 | 5.35 | 5.39 | 5.85 | 5.39 |
| I-8 | A6 6.67 | 6.80 | 6.78 | 6.68 | 6.71 | 7.30 | 6.69 |
| I-9 | C7 8.00 | 8.26 | 8.22 | 8.11 | 8.07 | 8.59 | 8.02 |
| I-10 | 9.77 | 9.72 | 9.63 | 9.48 | 10.19 | 9.37 | |
| I-11 | 11.36 | 11.34 | 11.08 | 10.88 | 11.61 | 10.74 | |
| I-12 | 12.92 | 12.80 | 12.61 | 12.26 | 12.25 | ||
| I-13 | 14.51 | 14.39 | 13.75 | 13.82 | |||
| I-14 | 16.14 | 15.11 | |||||
| I-15 | 17.76 | 16.53 | |||||
TABLE V. Relative frequencies of the first and second groups of some arbitrary tuned and untuned bells. The third Eijsbouts bell is untuned. Bell parameters in the upper part of the table show how sensitive bell frequencies are to small changes in bell geometry.
The upper part of the table gives important parameters for each bell. The strike note or nominal pitch, which will be discussed shortly, is here calculated as being one octave below the frequency of the nominal (I-4). The lower part of the table shows the relative frequencies of important partials. As many as possible partials of group I are listed, together with the hum, fundamental, fifth (II-3) and decime (II-4). The second column shows partials of the ideal bell, in musical notation as well as in relative frequency notation. This ideal bell is just a model, since there are no known bells with exactly these partial frequency ratios. The next three columns represent three Eijsbouts bells, where the first two were tuned and the third one was not. The last three columns contain some arbitrary old bells. One notices the different ways of structuring the first group of partials in these bells. Bells are characterized by close or by wide positions of overtones. Further, one notices that none of the bells has a correct (ideal) double octave (I-6); only the bell represented in the last column comes close to the relative frequency of 4.00. This bell, however, has other defects that are not made up for by the near-correct double octave. The most remarkable feature of the information given in this table is the fact that only very little alteration of the bell’s profile causes the occurrence of significant differences within the first group of partials. This once more underlines the necessity to attach as much geometric data as possible to tone recordings of a bell.
A very important perceptual feature of a bell’s sound is its strike note, which can be defined as a perceptual interpretation of the total sound during the strike in the form of a pitch sensation with a particularly sharp and metallic timbre. This pitch is typically found one octave below the nominal and does not seem to have a direct relation with the partial which is usually called the “fundamental.” This octave rule (Lehr, 1976) provides a good approximation in a well-tuned bell, although more recen1 investigations with electronically synthesized or recorded bell sounds suggest that, besides the nominal (I-4), the duodecime (I-5) and the double octave (I-6) are also mediators of the strike tone sensation (Schouten and ‘t Hart, 1965; Greenhough, 1976). Sometimes, in large bells, a secondary strike note is heard which is often one-fourth above the primary strike note. Measurements by Arts (1939) indicated that the double decime (I-7) plays a crucial role in forming this pitch sensation, whereas a later study (Schouten and ‘t Hart, 1965) suggests that this secondary strike note is mediated by partials I-6 through I-9 which typically show a frequency relation very close to 3:4:5:6. Furthermore, there is plenty of psychophysical evidence that deviation of partial frequencies from a harmonic relation weakens the sensation of pitch or makes it ambiguous (Schouten et al., 1962 ), and that the lower partials are the strongest conveyors of this (fundamental) pitch percept (Houtsma and Goldstein, 1972) . This suggests that the objective of a clear and unambiguous strike note is an additional reason why the lower partials of group I must be tuned so carefully.
The virtual pitch theory of Terhardt (Terhardt et al., 1982) is the only theory on pitch perception of complex tones that is developed in sufficient detail to make predictions about perceived strike notes of bells. This theory makes no assumptions in advance about which bell partials do or do not contribute to the pitch of the strike note, but considers, in principle, all acoustically available partials. With the aid of specific pitch shift, mutual masking, and loudness rules, the set of acoustically available spectral frequencies is reduced to a (much smaller) set of relevant spectral pitches, from which virtual pitches are derived by subharmonic division. The theory determines for each bell tested a number of possible virtual pitches, each having a perceptual “weight” or salience factor. This theory was recently tested on a series of pitch matches made to 137 different historical church bells by 11 different subjects (Terhardt and Seewann, 1984). For close to 80% of the bells, the strike note was found correctly predicted by the theory.
The grouping of bell partials lends itself also to a further description of the character of a bell. The timbre of a bell may not only be defined by the partial intensities and the relations between tones of the base chord, but also by the structure of the spectrum of each group by itself and the spectral positions of the groups relative to each other. Each group has tones with similar properties in the tone spectrum. Those of the first group dominate, while the others can be considered an additional feature. A compact chord structure of the first group, for instance, will undoubtedly be expressed in the timbre of the bell. In that context, the spectral position of the second group might appear much lower than usual. If this second group has a wide chord structure, the timbre is not only determined by the character of the base chord, in which the position of 1he fifth II-3 would be too low, but also by the higher tones of the second group. More listening tests will have to be carried out to investigate this further.
Acknowledgements
The author wants to express his thanks to J. H. G. van den Berk for his interest and valuable commentary during this study, and for the many conversations in which several ideas, mentioned in this paper, were born. The author is also indebted to A. J. M. Houtsma, T. D. Rossing, and A. H. Benade for their valuable contributions to the manuscript.
note 1 In this paper, the note A4 is taken as 440Hz.
note 2 In the English speaking countries, this type of bell is generally called a Flemish bell. Historically this name is incorrect, as the minor octave bell in this pure form was cast for the first time in The Netherlands by Hemony in 1644.
note 3 The bell is called after its strike note, so a C5 bell has a strike note of C5, a nominal of C6, and a hum note of C4.
Arts, J. (1939). “The sounds of bells: The secondary strike note.” J. Acoust. Soc. Am. 10, 327-329.
Federhofer, K. (1950). Dynamik des Bogentragers und Kreisringes (Springer, Vienna).
Geyseghem, V. van (1935) Congress of Carilloneurs, Ottawa, 1935.
Greenhough, M. (1976). “The analysis and synthesis of bell sounds,” in Proceedings of the Institute of Acoustics Conference, September 1976.
Heuven, E. W. van (1949) . “Acoustical measurements on church bells and carillons,” Ph. D. thesis, Delft, The Netherlands.
Houtsma, A. J. M., and Golds1ein, J. L. (1972). “The central origin of the pitch of complex tones: Evidence from musical interval recognition,” J. Acoust. Soc. Am. 51 , 520-529.
Jones, A. T., and Alderman, G. W. (1933). “Component tones from a bell,” J. Acoust. Soc. Am. 4, 331-343.
Lehr, A. J. (1952). ‘”A general bell formula,” Acustica 2, 35-38.
Lehr, A. J. (1956). “De rijkdom van de klokkenklank,” Mens en Melodie 11, 379-383.
Lehr, A. J. (1976). Leerboek der Campanologie (Nat. Beiaardmuseum, Asten).
Rayleigh, Lord (1877). The theory of Sound (Macmillan, London; reprinted by Dover, New York, 1945), Vol. I.
Rayleigh, Lord (1890). “On bells,” Philos. Mag. 29, 1-17; reprinted in Scientific Papers of Lord Rayleigh (Dover, 1964). Vol. 3, pp. 318-332.
Schouten, J. F., Ritsma, R. J., and Cardozo, B. L. (1962). “Pitch of the residue,” J. Acoust. Soc. Am. 34, 1418- 1424.
Schouten, J. F., and ‘t Hart, J. (1965). “De slagtoon van klokken,” in Enkele Voordrachren over Muziek en Muziekinstrumenten, Ned. Akoest. Genootschap Publ. No. 7.
Slaymaker, F H., and Meeker, W. F. (1954). “Measurements on the tonal characteristics of carillon bells,” J. Acoust. Soc. Am. 26, 515-522.
Terhardt, E., Stoll, G., and Seewann, M. (1982). “Algorithm for extraction of pitch and pitch salience from complex tone signals,” J. Acoust. Soc. Am. 71, 679-690.
Terhardt, E., and Seewann, M. (1984). “Auditive und objective Bestimmung der Schlagtonhohe van historischen Kirchenglocken,” Acustica 54, 129-144.
Vas Nunes, A. (1909) “Experimenteel Onderzoek van Klokken van F. Hemony,” Ph. D. thesis, Amsterdam, The Netherlands.