This article provides a fascinating insight into an early scientific investigations into bell vibrations and sound. In it Rayleigh explains the phenomenon of doublets, though they are not named as such; shows that the strike note of a church bell is an octave below the nominal; and investigates the vibration modes of the five lowest partials.
The text of the paper is reproduced in its entirety, apart from the appendix which provides a mathematical description of the bending of a hyperboloid of revolution, of limited interest. The frontispiece of the original paper includes some errata, which for convenience have been edited into the text.
THE LONDON, EDINBURGH, AND DUBLIN
PHILOSOPHICAL MAGAZINE
AND
JOURNAL OF SCIENCE.
[FIFTH SERIES.]
JANUARY 1890.
1. On Bells. By Lord RAYLEIGH, Sec. R.S. (Communicated by the Author)
The theory of the vibrations of bells is of considerable difficulty. Even when the thickness of the shell may be treated as very small, as in the case of air-pump receivers, finger-bowls, claret glasses, &c., the question has given rise to a difference of opinion. The more difficult problem presented by church bells, where the thickness of the metal in the region of the sound-bow (where the clapper strikes) is by no means small, has not yet been attacked. A complete theoretical investigation is indeed scarcely to be hoped for; but one of the principal objects of the present paper is to report the results of an experimental examination of several church bells, in the course of which some curious facts have disclosed themselves.
In practice bells are designed to be symmetrical about a axis, and we shall accordingly suppose that the figures are of revolution, or at least differ but little from such. Under these circumstances the possible vibrations divide themselves into classes, according to the number of times the motion repeats itself round the circumference. In the gravest mode, where the originally circular boundary becomes elliptical, the motion is once repeated, that is it occurs twice. The number of nodal meridians, determined by the points where the circle intersects the ellipse, is four, the meridians corresponding (for example) to longitudes 0º and 180º being reckoned separately. In like manner we may have 6, 8, 10… nodal meridians, corresponding to 3, 4, 5… cycles of motion. A class of vibrations is also possible which are symmetrical about the axis, the motion at any point being either in or perpendicular to the meridional plane. But these are of no acoustical importance.
The meaning here attached to the word nodal must be carefully observed. The meridians are not nodal in the sense that there is no motion, but only that there is no motion normal to the surface. This can be best illustrated by the simplest case, that of an infinitely long thin circular cylinder vibrating in two dimensions. (‘Theory of Sound,’ ¶232.) The graver vibrations are here purely flexural, the circumference remaining everywhere unstretched during the motion. If we fix our attention upon one mode of vibration of n cycles, the motion at the surface is usually both radial and tangential. There are, however, 2n points distributed at equal intervals where the motion is purely tangential, and other 2n points, bisecting the intervals of the former, where the motion is purely radial. There are thus no places of complete rest; but the first set of points, or the lines through them parallel to the axis, are called nodal, in the sense that there is at these places no normal motion.
The two systems of points have important relations to the place where the vibrations are excited. “When a bell-shaped body is sounded by a blow, the point of application of the blow is a place of maximum normal motion of the resulting vibrations, and the same is true when the vibrations are excited by a violin-bow, as generally in lecture-room experiments. Bells of glass, such as finger-glasses, are, however, more easily thrown into regular vibration by friction with the wetted finger carried round the circumference. The pitch of the resulting sound is the same as that elicited by a tap with the soft part of the finger; but inasmuch as the tangential motion of a vibrating bell has been very generally ignored, the production of sound in this manner been felt as a difficulty. It is now scarcely necessary to point out that the effect of the friction is in the first instance to excite tangential motion, and that the point of application of the friction is the place where the tangential motion is greatest, and therefore where the normal motion vanishes”. (‘Theory of Sound,’ ¶234. That the rubbing finger and the violin-bow must be applied at different points in order to obtain the same vibration was known to Chladni.)
When the symmetry is complete, the system of nodal meridians has no fixed position, and may adapt itself so as to suit the place at which a normal blow is delivered. If the point of application of the blow be conceived to travel round a circle symmetrical with respect to the axis, say, for brevity, a circle of latitude, the displacement will make no difference to the vibration considered as a whole, but the effect upon an observer who retains a fixed position will vary. If the bell be situated in an open space, or if the ear of the observer be so close that reflexions are relatively unimportant, the sound disappears as nodes pass by him, swelling to a maximum when the part nearest to the ear is one of the places of maximum normal motion, which for brevity we will call loops. In listening to a particular note it would thus be possible to determine the number of nodal meridians by watching the variations of intensity which occur as the place of the blow travels round a circle of latitude.
In practice the symmetry is seldom so complete that this account of the matter is sufficient. Theoretically the slightest departure from symmetry will in general render determinate the positions of the nodal systems. For each number of cycles n, there is one determinate mode of vibration with 2n nodes and 2n intermediate loops, and a second determinate mode in which the nodes and loops of the first mode exchange functions. Moreover the frequencies of the vibrations in the two modes are slightly different.
In accordance with the general theory, the vibrations of the two modes as dependent upon the situation and magnitude of the initiating blow are to be considered separately. The vibrations of the first mode will excited, unless the blow occur at a node of this system; and in various degrees, reaching a maximum when the blow is delivered at a loop. The intensity, as appreciated by an observer, depends also upon the position of his ear, and will be greatest when a loop is immediately opposite. As regards the vibrations of the second mode, they reach a maximum when those of the first mode disappear, and conversely.
Thus in the case of n cycles, there are 2n places where the first vibration is not excited and 2n places, midway between the former, where the second vibration is not excited. At all 4n places the resulting sound is free from beats. In all other cases both kinds of vibration are excited, and the sound will be affected by beats. But the prominence of the beats depends upon more than one circumstance. The intensities of the two vibrations will be equal when the place of the blow is midway between those which give no beats. But it does not follow that the audible beats are then most distinct. The condition to be satisfied is that the intensities be equal as they reach the ear, and this will depend upon the situation of the observer as well as upon the vigour of the vibrations themselves. Indeed, by suitably choosing the place of observation it would be theoretically possible to obtain beats with perfect silences, wherever (in relation to the nodal system) the blow may be delivered.
There will now be no difficulty in understanding the procedure adopted in order to fix the number of cycles corresponding to a given tone. If, in consequence of a near approach to symmetry, beats are not audible, they are introduced by loading the vibrating body. By tapping cautiously round a circle of latitude the places are then investigated where the beats disappear. But here a decision must not he made too hastily. The inaudibility of the beats may be favoured by an unsuitable position of the ear, or of the mouth of the resonator in connexion with the ear. By travelling round a situation is soon found where the observation can be made with the best advantage. In the neighbourhood of the place where the blow is being tried there is a loop of the vibration which is most excited and a (coincident) node of the vibration which is least excited. When the ear is opposite to a node of the first vibration, and therefore to a loop of the second, the original inequality is redressed, and distinct beats may be heard even although the deviation of the blow from a nodal point may be very small. The accurate determination in this way of two consecutive places where no beats are generated is all that is absolutely necessary. The ratio of the entire circumference of the circle of latitude to the arc between the points represents 4n, that is four times the number of cycles. Thus, if the arc between consecutive points proved to be 45º, we should infer that we were dealing with a vibration of two cycles – the one in which the deformation is elliptical. As a greater security against error, it is advisable in practice to determine a larger number of points where no beats occur. Unless the deviation from symmetry be considerable, these points should be uniformly distributed along the circle of lattitude. (The bells, or gongs, as they are sometimes called, of striking clocks often give disagreeable beats. A remedy may be found in a suitable rotation of the bell about its axis.)
In the above process for determining nodes we are supposed to hear distinctly the tone corresponding to the vibration under investigation. For this purpose the beats are of assistance in directing the attention; but with the more difficult subjects, such as church bells, it is advisable to have recourse to resonators. A set of Helmholtz’s pattern, manufactured by Koenig, are very convenient. The one next higher in pitch to the tone under examination is chosen and tuned by advancing the finger across the aperture. Without the security afforded by resonators, the determination of the octave is in my experience very uncertain. Thus pure tones are often estimated by musicians an octave too low.
Some years ago I made observations upon the tones of various glass bells, of which the walls were tolerably thin. A few examples may be given :-
| I. | c’, | e”b, | c”’#. |
| II. | a, | c”#, | b”. |
| III. | f’#, | b”. |
The value of n for the gravest tone is 2, for the second 3, and for the third 4. On account of the irregular shape and thickness only a very rough comparison with theory is possible; but it may be worth mention that for a thin uniform hemispherical bell the frequencies of the three slowest vibrations should be in the ratios
1 : 2.8102 : 5.4316;
so that the tones might be
c, f’#, f”, approximately.
More recently, through the kindness of Messrs. Mears and Stainbank, I have had an opportunity of examining a so-called hemispherical metal bell, weighing about 3 cwt. A section is shown in fig. 1. Four tones could be plainly heard,
eb, f’#, e”, b”,
the pitch being taken from a harmonium.
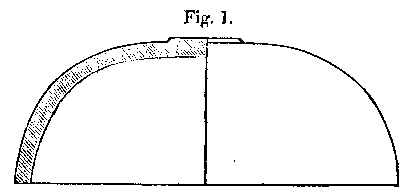
The gravest tone has a long duration. When the bell is struck by a hard body, the higher tones are at first predominant, but after a time they die away, and leave eb in possession of the field. If the striking body be soft, the original preponderance of the higher elements is less marked.
By the method above described there was no difficulty in showing that the four tones correspond respectively to n = 2, 3, 4, 5. Thus for the gravest tone the vibration is elliptical with 4 nodal meridians, for the next tone there are 6 nodal meridians, and so on. Tapping along a meridian showed that the sounds became less clear as the edge was departed from, and this in a continuous manner with no suggestion of a nodal circle of latitude.
A question, to which we shall recur in connexion with church bells, here suggests itself. Which of the various co-existing tones characterizes the pitch of the bell as a whole? It would appear to be the third in order, for the founders give the pitch as E nat.
My first attempts upon church bells were made in September 1879, upon the second bell (reckoned from the highest) of the Terling peal; and I was much puzzled to reconcile the pitch of the various tones, determined by resonators, with the effective pitch of the bell, when heard from a distance in conjunction with the other bells of the peal. There was a general agreement that the five notes of the peal were
f#, g#, a#, b, c#,
according to harmonium pitch, so that the note of the second bell was b. A tone of pitch a# could be heard, but at that time nothing coincident with b or its octaves. Subsequently, in January 1880, the b was found among the tones of the bell, but at much higher pitch than had been expected. The five gravest tones were determined to be
d’, a’#, d”, g”#+, b”;
so that the nominal note of the bell agreed with the fifth component tone, and with no graver one. The octaves are here indicated by dashes in the usual way, the c’ immediately below the d’ being the middle c of the musical scale.
Attempts were then made to identify the modes of vibration corresponding to the various tones, but with only partial success. By tapping round the sound-bow it appeared that the minima of beats for d’ occurred at intervals equal to 1/8 of the circumference, indicating that the deformation in this mode was elliptical (n=2), as had been expected. In like manner g”# gave n=3; but on account of the difficulty of experimenting in the belfry, the results were not wholly satisfactory, and I was unable to determine the modes for the other tones. One observation, however, of importance could be made. All five tones were affected with beats, from which it was concluded that none of them could be due to symmetrical vibrations, as, till then, had been thought not unlikely.
Nothing further worthy of record was effected until last year, when I obtained from Messrs. Mears and Stainbank the loan of a 6-cwt. bell. Hung in the laboratory at a convenient height, and with freedom of access to all parts of the circumference, this bell afforded a more convenient subject for experiment, and I was able to make the observations by which before I had been baffled. Former experience having shown me the difficulty of estimating the pitch of an isolated bell, I was anxious to have the judgement of the founders expressed in a definite form, and they were good enough to supply me with a fork tuned to the pitch of the bell. By my harmonium the fork is d”.
By tapping the bell in various places with a hammer or mallet, and listening with resonators, it was not difficult to detect 6 tones. They were identified with the following notes of the harmonium (In comparisons of this kind the observer must bear in mind the highly compound character of the notes of a reed instrument. It is usually a wise precaution to ascertain that a similar effect is not produced by the octave (or twelfth) above) :-
| e’, | c”, | f”+, | b”b, | d”’, | f”’. | |||||
| (4) | (4) | (6) | (6) | (8) |
As in the former case, the nominal pitch is governed by the fifth component tone, whose pitch is, however, an octave higher than that of the representative fork. It is to be understood, of course, that each of the 6 tones in the above series is really double, and that in some cases the components of a pair differ sufficiently to give rise to somewhat rapid beats. The sign + affixed to f” indicates that the tone of the bell was decidedly sharp in comparison with the note of the instrument.
I now proceeded to determine, as far is possible, the characters of the various modes of vibration by observations upon the dependence of the sounds upon the place of tapping in the manner already described. By tapping round a circle of lattitude it was easy to prove that (for each of the approximately coincident tones of) e’ there were 4 nodal meridians. Again, on tapping along a meridian to find whether there were any nodal circles of latitude, it became evident that there were none such. At the same time differences of intensity were observed. This tone is more fully developed when the blow is delivered about midway between the crown and rim of the bell than at other places.
The next tone is c”. Observation showed that for this vibration also there are four, and but four, nodal meridians. But now there is a well-defined nodal circle of latitude, situated about a quarter of the way up from the rim towards the crown. As heard with the resonator, this tone disappears when the blow is accurately delivered at some point of this circle, but revives with a very small displacement on either side. The nodal circle and the four meridians divide the surface into segments, over each of which the normal motion is of one sign.
To the tone f” correspond 6 nodal meridians. There is no well-defined nodal circle. The sound is indeed very faint, when the tap is much removed from the sound-bow; it was thought to fall to a minimum when the tap was about halfway up.
The three graver tones are heard loudly from the sound-bow. But the next in order, b”b, is there scarcely audible, unless the blow be delivered to the rim itself in a tangential direction. The maximum effect occurs at about halfway up. Tapping round the circle, we find that there are 6 nodal meridians.
The fifth tone, d”’, is heard loudly from the sound-bow, but soon falls off when the locality of the blow is varied, and in the upper three fourths of the bell it is very faint. No distinct circular node could be detected. Tapping round the circumference showed that there were here 8 nodal meridians.
The highest tone recorded, f”’, was not easy of observation, and I did not succeed in satisfying myself as to the character of the vibration. The tone was perhaps best heard when the blow was delivered at a point a little below the crown.
All the above tones, except f”, were tolerably close in pitch to the corresponding notes of the harmonium.
Although the above results seemed perfectly unambiguous, I was glad to have an opportunity of confirming them by examination of another bell. This was afforded by a loan of a bell cast by Taylor, of Loughborough, and destined for the church of Ampton, Suffolk, where it now hangs. Its weight is somewhat less than 4 cwt., and the nominal pitch is d. The observations were entirely confirmatory of the results obtained from Messrs. Mears’ bell. The tones were
| e’b-2, | d”-6, | f”+4, | b”b–b”, | d”’, | g”’; | |||||
| (4) | (4) | (6) | (6) | (8) |
the correspondence between the order of the tone and the number of nodal meridians being as before. In the case of d” there was the same well-defined nodal circle. The highest tone, g”’, was but imperfectly heard, and no investigation could be made of the corresponding mode of vibration.
In the specification of pitch the numerals following the note indicate by how much the frequency of the bell differed from that of the harmonium. Thus the gravest tone e’b gave 2 beats per second, and was flat. When the number exceeds 3, it is the result of somewhat rough estimation and cannot be trusted to be quite accurate. Moreover, as has been explained, there are in strictness two frequencies under each head, and these often differ sensibly. In the case of the 4th tone, b”b–b” means that, as nearly as could be judged, the pitch of the bell was midway between the two specified notes of the harmonium.
The sounds of bells may be elicited otherwise than by blows. Advantage may often be taken of the response to the notes of the harmonium, to the voice, or to organ-pipes sounded in the neighbourhood. In these cases the subsequent resonance of the bell has the character of a pure tone. Perhaps the most striking experiment is with a tuning-fork. A massive e’b (e on the c’=256 scale) fork, tuned with wax, and placed upon the waist of the Ampton bell, called forth a magnificent resonance, which lasted for some time after removal and damping of the fork. The sound is so utterly unlike that usually associated with bells that an air of mystery envelops the phenomenon. The fork may be excited either by a blow upon a pad (in practice it was the bent knee of the observer), or by bowing when in contact with the bell. In either case the adjustment of pitch should be very precise, and it is usually necessary to distinguish the two nearly coincident tones of the bell. One of these is to be chosen and the fork is to be held near a loop of the corresponding mode of vibration. In practice the simplest way to effect the tuning is to watch the course of things after the vibrating fork has been brought into contact with the bell. When the tuning is good the sound swells continuously. Any beats that are heard must be gradually slowed down by adjustment of wax, until they disappear.
Observations upon the two bells in the laboratory having settled the modes of vibration corresponding to the five gravest tones, other bells of the church pattern can be sufficiently investigated by simple determinations of pitch. I give in tabular form results of this kind for a Belgian bell, kindly placed at my disposal by Mr. Haweis, and for the five bells of the Terling peal. For completeness’ sake the Table includes also the corresponding results for the two bells already described.
| Mears, 1888. | Ampton, 1888. | Belgian Bell. | Terling (5), Osborn, 1783. | Terling (4), Mears, 1810. | Terling (3), Graye, 1623. | Terling (2), Gardiner, 1723. | Terling (1), Warner, 1863. |
| Actual Pitch by Harmonium. | |||||||
| e’ e” f”+ b”b d”’ f”’ | e’b-2 d”-6 f”+4 b”b-b” d”’ g”’ | d’-4 c”#-d” f”+1 a”-6 ….. | g-3 g’-4 a’+6 d”-3 f”#-2 | a+3 g’#-4 b’+6 d”#-e” g”#-6 | a#+3 a’+6 c”#+4 e”+6 a”# | d’-6 a’#-5 d”+8 g”#+(10) b”+2 | d’+2 b’+2 e” g”#+4 c”’#+3 |
| Pitch referred to fifth tone as c. | |||||||
| d bb eb+ ab c | c#-2 c-6 eb+4 ab–a c | c#-3 c#-4 eb+6 ab-3 c-2 | c#+3 c-4 eb+6 g–g# c-6 | c+3 bb+6 eb+4 f#+6 c | eb-6 b-5 eb+8 a+8 c+2 | c#+2 bb+2 eb g+4 c+3 |
It will be seen that in every case where the test can be applied it is the fifth tone in order which agrees with the nominal pitch of the bell. The reader will not be more surprised at this conclusion than I was, but there seems to be no escape from it. Even apart from of estimates of pitch, an examination of the tones of the bells of the Terling peal proves that it is only from the third and fifth tones that a tolerable diatonic scale can be constructed. Observations in the neighbourhood of bells do not suggest any special predominance of the fifth tone, but the effect is a good deal modified by distance.
It has been suggested, I think by Helmholtz, that the aim of the original designers of bells may have been to bring into harmonic relations tones which otherwise cause a disagreeable effect. If this be so, the result cannot be considered very successful. A glance at the Table shows that in almost every case there occur intervals which would usually be counted intolerable, such as the false octave. Terling (5) is the only bell which avoids this false interval between the two first tones; but the improvement here shown in this respect still leaves much to be desired, when we consider the relation of these two tones to the fifth tone, and the nominal pitch of the bell. Upon the assumption that the nominal pitch is governed by that of the fifth tone, I have exhibited in the second part of the above Table the relationship in each case of the various tones to this one.
One of my objects in this investigation having been to find out, if possible, wherein lay the difference between good and bad bells, I was anxious to interpret in accordance with my results the observations of Mr. Haweis, who has given so much attention to the subject. The comparison is, however, not free from difficulty. Mr. Haweis says (‘Times,’ October 29, 1878) :- “The true Belgian bell when struck a little above the rim gives the dominant note of the bell; when struck two-thirds up it gives the third; and near the top the fifth; and the ‘true’ bell is that in which the third and fifth (to leave out a multitude of other partials) are heard in right relative subordination to the dominant note.”
If I am right in respect of the dominant note, the third spoken of by Mr. Haweis must be the minor third (or rather, major sixth) presented by the tone third in order, which is so happens is nearly the same interval in all cases. The only fifth which occurs is that of the tone fourth in order. Thus, according to Mr. Haweis’s views, the best bell in the series would be Terling (1), for which the minor chord of the last three tones is very nearly true. It must be remarked, however, that the tone fourth in order is scarcely heard in the normal use of the bell, so that its pitch can hardly be of importance directly, although it may afford a useful criterion of the character of the bell as a whole. It is evident that the first and second tones of Terling (1) are quite out of relation with the higher ones. If the first could be depressed a semitone and the second raised a whole tone, harmonic relations would prevail throughout.
Judging from the variety presented in the Table, it would seem not a hopeless task so to construct a bell that all the important tones should be brought into harmonic relation; but it would require so much tentative work that it could only be undertaken advantageously by one in connexion with a foundry. As to what advantage would be gained in the event of success, I find it difficult to form an opinion. All I can say is that the dissonant effect of the inharmonious intervals actually met with is less than one would have expected from a musical point of view; although the fact is to a great extent explained by Helmholtz’s theory of dissonance.
One other point I will touch upon, though with great diffidence. If there is anything well established in theoretical acoustics it is that the frequencies of vibration of similar bodies formed of similar material are inversely as the linear dimensions – a law which extends to all the possible modes of vibration. Hence, if the dimensions are halved, all the tones should rise in pitch by an exact octave. I have been given to understand, however, that bells are not designed upon this principle of similarity, and that the attempt to do so would result in failure. It is just possible that differences in cooling may influence the hardness, and so interfere with the similarity of corresponding parts, in spite of uniformity in the chemical composition of the metal; but this explanation does not appear adequate. Can it be that when the scale of a bell is altered it is desirable at the same time to modify the relative intensifies, or even the relative frequencies, of the various partials?
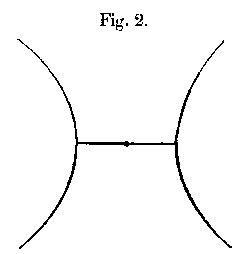
Observations conducted about ten years ago upon the manner of bending of bell-shaped bodies – waste-paper baskets and various structures of flexible material – led me to think that these shapes were especially stiff as regards the principal mode of bending (with four nodal meridians) to forces applied normally and near the rim, and that possibly one of the objects of the particular form adopted for bells might be to diminish the preponderance of the gravest tone. To illustrate this I made calculations, according to the theory of the paper already alluded to, of the deformation by pure bending of thin shells in the form of hyperboloids of revolution, and in certain composite forms built up of cylinders and cones so as to represent approximately the actual shape of bells. In the case of the hyperboloid of one sheet (fig. 2), completed by a crown in the form of a circular disk through the centre, and extending across the aperture, it appeared that there was no nodal circle for n=2. The investigation is appended to this paper.
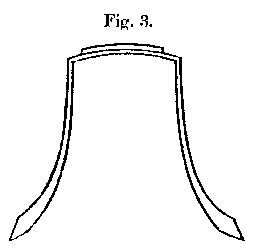
The composite forms, figs. 4 and 5, represent the actual bell (fig. 3, copied from Zamminer, Die Musik und die musikalischen Instrumente. Giessen, 1855) as nearly as may be. At the top is a circular disk, and to this is attached a cylindrical segment. The expanding part of the bell is represented by one (fig. 4), or with better approximation by two (fig. 5), segments of cones. The calculations are too tedious to be reproduced here, but the results are shown upon the figures. In both cases there is a circular node N for n=2, not far removed from the rim, and in fig. 5 very nearly at the place which represents the sound-bow of an actual bell. In the latter case there is a node N’ for n=3 near the middle of the intermediate conical segment.
The nodal circle for n=2 has been verified experimentally upon a bell constructed of thin sheet zinc in the form of fig. 5. The gravest note, G#, and the corresponding mode of vibration, could be investigated exactly in the manner already described. In each mode of this kind there were four nodal meridians, and a very well defined nodal circle. The situation of this circle was not quite so low as according to calculation; it was almost exactly in the middle of the lower conical segment. By merely handling the model it was to recognize that it was stiff to forces applied at N, but flexible higher up, in the neighbourhood of N’.
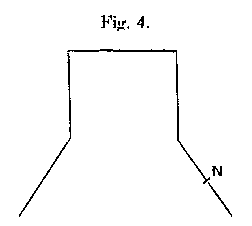
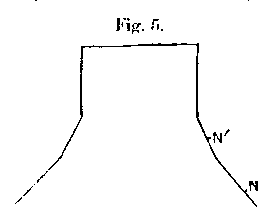
It is clear that the actual behaviour of a church bell differs widely from that of a bell infinitely thin; and that this should be the case need not surprise us when we consider the actual ratio of the thickness at the sound-bow to the interval between successive nodal meridians. I think, however, that the form of the bell does really tend to render the gravest tone less prominent.
(An Appendix On the bending of a Hyperboloid of Revolution follows in the original paper. It provides a mathematical treatment of modes of vibration of a hyperboloid.)