This paper was originally published as “Auditive und objective Bestimmung der Schlagtonhöhe von Historischen Kirchenglocken” in Acustica 1984 Vol. 54 pp. 129-144. I translated it from the original German into English in autumn 2003. It is published here with the kind permission of Prof. Ernst Terhardt.
One of the objectives of work described in the paper was to test an algorithmic method of pitch determination. However, the paper also includes important information on the strike pitches of bells and how they are generated.
Contents of the paper are as follows:
Summary
1. Introduction
2. Partial tone structure and pitch analysis
2.1 Natural modes of vibration and partial tones
2.2 Primary pitch perceptions (spectral pitches)
2.3 Virtual pitches
2.4 The nature of the strike pitch
3. Aural determination of the strike pitches
3.1 Comparison method (adjustment test)
3.2 Vocal reproduction (reproduction experiment)
3.3 Comparison of the two methods
4. Results
4.1 Aurally measured strike pitches
4.2 Algorithmically determined strike pitches
5. Final conclusions
References
Aural and algorithmic determination of the strike note of historical church bells
by E. Terhardt and M. Seewann
Chair for Electroacoustics, Technical University of Munich
Dedicated to the 60th birthday of Professor E. Zwicker, Doctor of Engineering.
Summary
If a bell sound is capable of evoking a predominant pitch sensation, one assigns a so-called strike note to it. Depending on various characteristics of the sound, the strike note can be the same pitch as a partial tone or can be a virtual pitch. In two different experiments with 15 and 11 test subjects the strike notes were aurally determined for 17 and 137 historical church-bells. With 3% of the bells, no significant strike note could be determined. With 69%, there was a dominant strike-note which was unambiguous with respect to musical note name, though not necessarily with respect to octave position. To the extent that the partial tones can be arranged in today’s usual pattern (Hum, Prime, Tierce, Quint, Nominal, Tenth, Twelfth, Octave Nominal), the octave position of the strike note is often ambiguous as to the Hum vs. Prime position. Fine tuning of the strike note on the average is sharp relative to the Prime, and flat relative to the Nominal. Algorithmic determination of the strike notes was carried out with the procedure of Terhardt et al. [18]. With 79% of the 137 bells, the musical note-name of the strike notes was correctly identified by the procedure. If the strike note of a bell is sufficiently pronounced, it can be determined algorithmically with almost perfect performance. As a criterion of pitch strength, the calculated pitch weight is used. If it exceeds the average value of the historical bells investigated (0.62), this is sufficient for a successful determination. It is shown that the algorithmic procedure also meets realistic expectations for determination of the octave position and fine tuning of the strike note.
1. Introduction
The strike note heard when a bell is struck is still considered to be an unsolved mystery of acoustics. By strike note is meant the dominant musical pitch of the bell sound. Depending upon the nature and sound quality of a bell the strike note can be more or less pronounced or unique. It is because of the strike note that a musical note can be ascribed to a bell when it is struck. Experience shows that the strike note phenomenon is closely associated with the sound of the bell during the first second after the clapper impact [4, 6].
The term “strike note” is in certain respects unfounded and misleading. We therefore intend to describe what is heard as the “strike pitch”. On the one hand this preserves the connection to the original designation, and on the other hand we can maintain the distinction between tone and pitch: A tone is in the language of acoustics a special sound, i.e. a physical thing. In contrast to this the pitch is a characteristic of a tone, i.e. its felt height, and is a sensory (subjective) thing. The solution of the “strike note mystery” lies not in finding a tone, but in explaining how the described pitch sensation arises from the physical sound. This formulation of the problem makes it clear that it does not cover only an isolated, bell-specific mystery, but rather a special case of a general psycho-acoustical problem, that of explaining the pitch perception of any waveform.
Bell sounds represent a special challenge to any pitch theory. While one can find directly identifiable features of the pitch with most tonal waveforms of daily life either in the time function or in the amplitude spectrum (or in both), this is not generally the case with bell sounds. In general there is neither a periodicity of the sound pressure time function at the strike pitch, nor a partial tone extractable by spectrographic analysis, whose magnitude is sufficient to account for the strike pitch. Nor are strike pitches explicable as aural difference tones (“internal partial tones” created by non-linearities in the ear). Indeed it has long been proved by psycho-acoustical experiments that neither a partial tone is required in the spectrum, where a pitch is perceived [12, 9], nor need the waveform have a periodicity at the appropriate frequency [9]. Psycho-acoustic theory shows that instead, pitch perception is generally to be understood as a process of spectral shape perception [15, 9]. This explanation extends to the strike pitches of bells, and the theory can provide a basic scientific explanation of observed effects.
However, so far only limited experience is available regarding the extent to which existing pitch theories give reliable and exact determination of strike pitch. The work documented here makes a particular contribution to this question. We report on the determination of the strike pitch for a total of 137 historical church bells from the Lower Franconia area dating from 1249 to 1845. Understandably older bells often only have a moderate sound quality and the clarity of their strike pitch often leaves much to be desired. Such bell sounds therefore provide a particularly stringent test of algorithmic strike pitch determination procedures. Tape recordings of the sounds of the individual bells [footnote – We thank Dr. M. Nitz (Bavarian National Office for the Care of Monuments, Munich) who made the tape recordings as part of the art-historical documentation of the bells] were aurally judged by 15 test subjects, and were also subjected to a pitch analysis based on virtual pitch theory [15]. The procedure was recently described in detail [18]. The second type of analysis is called algorithmic strike pitch determination, because it uses a fixed, specified algorithm. Particularly detailed aural pitch measurements using the comparison method were carried out by a sub-group on 17 bells, as has already been briefly reported [13]. The data obtained has been further analysed in this study and compared with the appropriate algorithmic results. First, summarised below as a starting point for the actual investigations, are the significant physical and aural sound features of the bells.
2. Partial tone structure and pitch analysis
Some of the pitch sensations caused by bell sounds are of “primary” type, i.e., they correspond directly to certain partial tones in the sound; these are called spectral pitches. A second type of pitch sensation results from holistic perception of the sound (aural effect); these are called virtual pitches [15]. The dominant strike pitch under various conditions can be either a spectral or a virtual pitch. Both spectral pitches and virtual pitches depend on the partial tone spectrum. The nature of this dependency is described by the detailed pitch computation method already referred to [18]. In the description below the results and criteria of the underlying psycho-acoustical pitch theory are applied to bell sounds. The most important result of this work is validation of the procedure for algorithmic pitch analysis suggested by us; in addition, a contribution is also made to the general understanding of perception of bell sounds. Various different results of the investigations are explained and illustrated.
2.1. Natural modes of vibration and partial tones
A bell represents a vibratory system, which possesses a multiplicity of natural modes of vibration. The frequencies and attenuation factors of these modes depend only on the form and the material of the bell, if one ignores non-linear effects (dependency of the natural frequencies on the amplitude) and the effect of temperature (the measurements of Jones [5] and Stueber and Kallenbach [14] show that the temperature coefficient of the natural frequencies amounts to approximately 1.5 x 10-4 per deg. C with bronze bells). The natural frequencies, when stimulated by the blow of a clapper, have a large initial oscillation of very short duration with a large bandwidth. The initial amplitude of each natural oscillation depends on the strength and the place of the clapper impact. This set of natural oscillations radiated as airborne sound produces a waveform, which the sound of the bell is called in the environment. The sinusoidal spectral components of the sound, which can be found by spectrographic analysis, are called partial tones. Their frequencies correspond with good approximation to those of the appropriate natural modes of vibration of the bell. To the amplitudes this does not apply; that is, the partial tone amplitudes measured in the sound signal depend not only on the amplitudes of the natural oscillations, but additionally on the sound radiation and propagation conditions. Nevertheless, the sound signal arriving in the ear is the authoritative source of the audible sound impression, so that it is realistic to describe bell sounds by the partial tone spectra of the sound signals in the environment instead of giving merely the partial frequencies. The partial frequencies determine the sound impression to a considerable degree, and are in some sense “invariant parameters” of a bell, so that they rightfully play a large role in discussions of a bell’s acoustic characteristics.
In the procedure for algorithmic pitch analysis the partial frequencies and amplitudes are determined from a digitally calculated Fourier spectrum (FFT) of the sound pressure time function (with time window 80 ms; bandwidth 5 kHz), by selecting the most prominent amplitude maxima of the quasi-continuous spectral function [18]. The spectrographic analyses on which all the algorithmic determinations were performed, were made with a delay of 40 ms after the clapper blow, in order on the one hand to capture the sound essentially at the beginning, while on the other hand avoiding the initial clapper impact noise. The sound signals were recorded in the bell chamber from approximately 2 m. distance on tape. The bell was rung by hand with its own clapper.
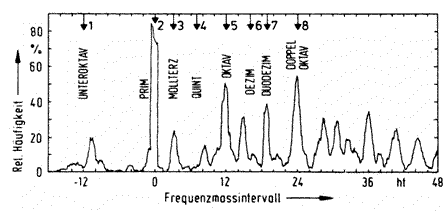
Fig. 1. Frequency of occurrence of audible partial frequencies in 137 bells in each semitone interval, plotted against the centre frequency of the “window”. The frequency in semitones along the abscissa is defined by the frequency measure interval of 12 x log2 (f/fs), whereby the frequency is related to the calculated strike pitch frequency; the latter corresponds to the zero point of the abscissa. The ordinate shows the proportion of the total bells with a partial at that frequency. The numbered arrows at the top margin mark the ideal position of the partial tones.
The relationship between the partial frequencies does not follow a simple, natural pattern, and depends on the shape and cross section of the bell. In modern church bells the first eight partial frequencies are required to be in the ratios 1 : 2 : 2.4 : 3 : 4 : 5 : 6 : 8 and these ratios are achieved with good approximation [2, 11]. Older church-bells can deviate substantially from these ratios. Fig. 1 illustrates the frequency ratios observed by us in 137 historical bells. The calculated strike pitch was taken as the frequency reference, and the deviation of the frequency of each observed partial tone from it was indicated by the frequency measure interval of 12 x log2 (fP / fS) semitones. (fP = partial tone frequency; fS = appropriate strike pitch frequency). The ordinate shows the frequency of occurrence of individual partial frequencies within a semitone-wide “window”; the window was continuously shifted along the abscissa. Only those partial tones, which are separately audible in the sound (see section 2.2.) were considered. The ideal partial frequencies are shown in the top margin by perpendicular arrows and the usual designations of the partial tones by numbers or names are indicated.
The diagram shows that the partial tone structure of older bells in many individual cases deviates considerably from the ideal, although it is clear that first eight partial tones tend at least to approximate to it. The frequency of the first partial tone deviates substantially from an octave below the second (or the strike pitch) and tends to be either a seventh or a ninth (see [2, 11, 19]).
If with all the examined bells the pitch of the second partial tone were identical to the strike pitch, a vertical rectangle of width 1 semitone and height 100% would appear, positioned symmetrically about the zero point in the diagram. The actual position, shape and height of the distribution show that there is indeed a high measure of agreement between the pitch of the second partial tone and the strike pitch. However it is clear that the second partial tone, if in this area, is usually below rather than above the strike pitch.
The two octave tones (Nos. 5 and 8) were audible at the ideal frequencies in approximately half of the cases, as can be inferred from Fig. 1. The frequency maxima belonging to the Tierce, Quint, Tenth and Twelfth are markedly smaller. Nonetheless there are unique maxima for the Tierce and Twelfth in a position corresponding well with the desired values. Clear deviations from the ideal can be seen for the Quint (4th partial tone) and the Tenth (6th partial tone). The 4th partial tone shows a pronounced tendency towards a sixth (8 – 9 semitones), and the 6th Partial tone tends to a minor tenth (15 semitones) in place of the major tenth preferred nowadays (16 semitones). Above 24 semitones the frequency maxima show similar musical intervals. They clearly tend to form a major chord based on the respective partial tone (major third, fifth, octave).
2.2. Primary pitch perceptions (spectral pitches)
Each of the partial tones can cause a consciously perceptible pitch (a spectral pitch), if it is not masked by neighbouring partial tones or noise. In the pitch computation method the degree of audibility of a spectral pitch is described by the so-called level surplus. This level surplus is the difference between the volume of the partial tone concerned and that volume, which corresponds to the masking effect of all remaining partial tones or noise [18, 16]. If the level surplus is less than zero, then the partial tone concerned is regarded as inaudible in the sense that it does not cause a perceptible pitch. In earlier experiments it was shown that the procedure supplies in this regard quite reliable forecasts of the audibility of partial tones [16]. In the case of the 137 bells we examined, the average number of audible partial tones found by the computation method was 8.1. These usually included the eight partial tones required by modern tuning standards.
The pitch sensation is thus always ambiguous, because individual spectral pitches can stand out more or less strongly according to their level surplus. One generally hears a sound, which is a musical chord assembled from pure tones with “percussion-like” amplitude envelopes. This chord is made up of intervals which musical theory would say were dissonant because of the combination of major third and Tierce. The fact that bell sounds in this sense have the character of a musical chord, explains in part the attractive effect of these sounds and justifies the term “bell music” used by Griesbacher [3].
The weight, with which a certain partial tone contributes to the sound effect, depends not only on the degree of audibility (that is, the level surplus), but also on the absolute partial frequency. Hearing perception does not give the same weight to all audible partial tones, but prefers those spectral pitches situated in a dominant frequency range [8, 10]. This range extends approximately from 500 cycles per second to 1500 cycles per second [15]. In the pitch computation method this is taken into account, as the level surplus of the individual partial tones is weighted, so that the importance of a partial tone depends on both its level surplus and its partial frequency.
The phenomenon of spectral dominance has great importance for the tonal evaluation of bells. For example, if a bell has a strike pitch in the one-primed octave [translator’s note: the octave from middle C upwards] (which is often the case for church bells), then the first partial tone falls below the dominant frequency range. The first partial then plays a reduced role in sound perception even if it is actually well audible. In particular its tuning is not then critical. Then at the same time the Nominal, Tenth and Twelfth will lie more or less completely in the dominant range, so that they are of large importance. They then play a significant role in forming the virtual pitches of the bell. On the other hand, if the strike pitch is at the centre of the dominant range or higher, then the partial tones above the second fall in importance. They play a diminishing role in determining the strike pitch the higher they are above the critical region (that is, over 1500 cycles per second). The strike pitch is then formed from the 2nd or 1st partial tone alone and is almost certainly a spectral pitch (for this see [1, 3]).
In large agreement with the experiences of the bell specialists one can therefore state, due to the described psycho-acoustical factors, that substantial aspects of the sound perception of a bell are not only determined by relative frequencies of the partial tones, but to a considerable degree also by their absolute frequencies (the general tone position).
For the evaluation of the fine tuning of spectral pitches, the phenomenon of pitch shift is of importance. This effect arises because the spectral pitch of a partial tone of fixed frequency to some extent depends on its intensity of sound and particularly on the strength of other neighbouring partial tones. This circumstance can be expressed also in such a way that the equivalent pitch is not identical in all cases with the partial frequency. Rather both can differ by a few parts per thousand or per hundred from each other, and this difference is called pitch shift [15]. Pitch shifts are fundamentally the same for all persons with normal hearing, but can clearly differ in amount from person to person. This means that pitch measurements by comparison with a tone (for example a tuning fork) can result in systematically different results depending on which person takes the measurement, without one being able to say that one measurement result is more “correct” than another. It follows that an algorithmic pitch determination procedure which considers pitch shifts can only supply a representative average value and indicate the shift direction. We only have limited experience so far of the accuracy and reliability of the procedure we use. This means that one must allow a considerable error tolerance to the relevant algorithmic forecasts. However, since pitch shifts are a “second order effect”, this is acceptable, particularly since our experience is that the results of the procedure are more exact than they would be if the pitch shifts were not allowed for at all.
2.3. Virtual pitches
If by a complex tone one understands a sound which creates several pitch sensations at the same time, in contrast to a single note, then one can say that bell sounds usually represent a border line case; they are both complex tone and single note at once. The nature of the pitch perception of individual partial tones described above essentially constitutes the complex tone character. The only exception is bells with a high pitch, for their first partial tone alone determines the pitch if its intensity and frequency position permits. There is however another pitch perception mechanism, which is characterized by its integrating effect, in such a manner that a “note” is heard under certain circumstances from a complex partial tone spectrum, with a single dominant pitch, without any one partial tone prevailing. This perception mode is not the exception but the rule in acoustic communication with language and music. It is for example responsible for the fact that the complex partial tone spectrum of the human voice has a uniform pitch sensation. This type of pitch sensation is called virtual pitch. Since the partial tone spectrum of the bells indicates a certain similarity with the inharmonious structured spectra of periodic acoustic vibrations (for example of the voice and other musical tones), it is understandable that a bell sound can also cause more or less pronounced virtual pitches. Work by Schouten [12] already referred to demonstrates this.
Using our pitch computation method the virtual pitches are found by first determining the audible and spectrally weighted spectral pitches of the partial tones, as described in the preceding section. Next, that basic pitch is identified, which corresponds to the hypothetical lowest partial tone of a harmonic series, such that actual partial frequencies could be regarded as a coincidental selection of frequencies from the harmonic series. The procedure used to find this basic pitch is called “sub-harmonic coincidence detection” [18 ]. The procedure supplies a number of virtual pitches, in agreement with numerous psycho-acoustical measurement results, with a weight number specifying their relative importance. This weighting depends on the weight of the spectral pitches involved, as determined previously, as well as on their “harmonicity”, i.e. on the accuracy with which they fit into the harmonic series mentioned above.
The fine tuning of a certain virtual pitch is directly linked with the spectral pitch of the determining partial tone. For example if the second partial tone is near A’ (440 cycles per second) or below, then the succeeding partial tones fall more or less completely in the dominant spectral region. That is, they are candidates for the development of virtual pitches, if they have a sufficiently large level surplus. The fifth and sixth partial tones generate a virtual pitch in the region of the second, because they are in a harmonic series with a fundamental close to this partial. If the fifth partial tone possesses the most pronounced spectral pitch, which because of its favourable physical prerequisites (strength, and position within the dominant spectral region) is probable, then its spectral pitch determines the fine tuning of the virtual pitch an octave below. This directly explains the frequently-made observation that the strike pitch corresponds better in its fine tuning with that of the fifth partial tone rather than the second, in whose proximity it is situated [1, 2, 4, 6].
In addition, something similar applies to the fine tuning of virtual pitches as with spectral pitch: there are pitch shifts, which arise because the pitch-equivalent frequencies are not all exact integral divisors of the determining partial tone frequency. The algorithmic computation method includes a calculation to cater for this effect.
2.4. The nature of the strike pitch
The aural effect of tone caused by a bell sound can be ascribed both to spectral pitches and to virtual pitches. The first represent the “actually present” partial tones, and the latter the “tonal meaning” of them. A fundamentally false conclusion would be to be assume that the spectral pitches possess a higher degree of reality than the virtual pitches, or that the latter are a “psychological illusion” (for this see [7]). Although the connection between a spectral pitch and the accompanying partial tone frequency is formally essentially easier than that between a virtual pitch and the partial tones generating it, however, with both pitch kinds there is the basic difference between stimulus and effect, that is of the world of physical occurrences and that of the sensations. A spectral pitch is by no means less “psychological” than a virtual pitch.
In the perceived bell sound the various spectral and virtual pitches compete over which prevails at an instant in the conscious experience. Following our calculation procedure, the pitch which shows the biggest calculated weight is regarded as dominant and is therefore the strike pitch, whether it is a spectral pitch or a virtual pitch. Experience shows that pitches are virtual pitches in the area of the one-primed octave [translator’s note: the octave from middle C upwards] and below, while higher strike pitches are as a rule spectral pitches. Therefore, one can distinguish the following three cases:
1. The strike pitch is identical in nature to the spectral pitch of a partial tone (this can often be the second partial, or the first in bells of higher pitch); the strike pitch is then naturally also identical in ‘pitch height’ to the spectral pitch concerned. The quantity of such cases explains the considerable extent, as demonstrated in Fig. 1, to which the frequency of the second partial tone corresponds exactly to the strike pitch.
2. The strike pitch is a virtual pitch and is situated more or less near to the spectral pitch of a partial tone (with church-bells, with a typical partial tone pattern, this is the second or first partial tone). The quantity of these cases explains the extent to which, in Fig. 1, the strike pitch is close to the second partial tone but not co-incident with it.
3. The strike pitch is a virtual pitch and is not situated near any partial tone. These cases account for the deficit by which the number of cases against the second partial tone falls below 100% in Fig. 1.
For the 137 historical church bells studied, 12% fell into case 1, 77% into case 2 and 11% into case 3.
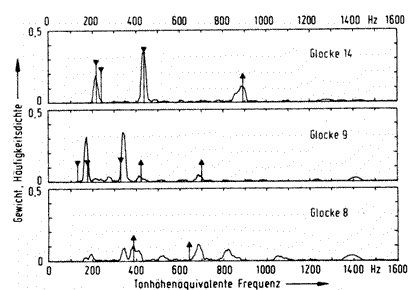
Fig. 2. Strike pitches determined aurally by an adjustment test (the smooth curve), or algorithmically (vertical lines with triangle). The frequency density (ordinate) refers to the results from the hearing comparison and gives the relative number of values which were found in a window 0.2 frequency groups wide, whose centre frequency was continuously shifted (abscissa). The reference value of the frequency density is the total number of settings (N = 147). The algorithmically calculated strike pitches indicated by the points of the triangles mark the pitch-equivalent frequency (abscissa) or calculated weight (ordinate). The weight specifications on the ordinate should be multiplied by 2 to get the actual calculated values. Only those calculated pitches are shown whose weight amounts to at least half of the maximum value, or at least a value of 0.2.
Fig. 2 shows three examples of pitch determination by the computation method. The points of the vertical triangles show for the significant calculated pitches the frequency (abscissa) and weight (ordinate). Triangles pointing upward mark the spectral pitches, and those downward the virtual pitches. Pitches of a bell are taken as significant if their weight is at least half the maximum weight occurring for the bell, and also at least 0.2 in value (note that the weights in Fig. 2 are shown at half their true values). The strike pitches in these examples which have the largest weight, correspond to frequencies of 442 cycles per second with bell 14, 425 cycles per second with bell 9 and 388 cycles per second with bell 8.
In a carillon or chime the strike pitches of the individual bells are usually used for melodic purposes. In the sound of an individual bell, as well as in a church tower ring, strike pitches can also be the tonics of musical chords. As explained elsewhere [17], musical chord tonics can explain the Rameau “fundamental bass” of music theory as virtual pitches and be psycho-acoustically justified. This ambivalence in the nature of the strike pitch gives a further explanation of the attractive effect of bell sounds on the hearing.
3. Aural determination of the strike pitches
Some methodical problems arise from the large number of bells to be examined, the tonal ambiguity of the sounds, and also the fact that the relative amplitude of the partial tones changes as the sound dies away. The pitch ambiguity means that all the possible strike pitches must be encompassed. The changes over time of the partial tone spectrum means that, in addition, clarification was needed of the extent to which pitch allocation for different time segments of the sound was different. Because of the large amount of time needed to clarify these questions, a group of 17 bells was selected with the criterion that they cover the whole quality range from melodious to dissonant. The pitch sensations caused by these bells were measured using the comparison method [20] and displayed in histograms. The experience gained from this test led to a simpler and less time-consuming method for examining the majority of the bells, i.e. the “vocal reproduction” approach. The two methods are described below.
3.1. Comparison method (adjustment test)
After listening to a bell sound, the test subject adjusts the frequency of a pure tone so that the pitch impression of the comparison tone corresponds to the pitch of the preceding test sound, which was spontaneously heard and then kept uppermost in the mind. The frequency of the pure tone then serves as a direct measure of the strike pitch of the test sound. In our experiments the test sound and comparison tone were repeated, until the test subject was content with the alignment and indicated this to the test manager, who then noted the comparison audio frequency. The test subject adjusted the frequency setting using a helipot with no scale. Sufficient repetitions of the adjustment procedure were performed to provide an indication of the statistical distribution of the adjusted comparison audio frequencies and thus the assigned pitches.
In order to decide the influence of different time periods of the bell sound, the adjustment test was executed in three parts:
- on the whole sound, i.e. a full three seconds of time beginning at the impact;
- on the initial sound, i.e. a time segment 100 ms long beginning at the impact; and
- on the tail of the sound, i.e. a time segment 100 ms long beginning 600 ms after the impact.
The test sounds were played with a peak volume level of 70 phons, the comparison tone at a volume of 60 dB. The sounds were presented to each test subject separately with DT48 binaural free field equalised headphones in a sound-isolated measurement room. For each bell, three tests were done on the initial sound and the tail of the sound, and five tests on the whole sound. The sounds were presented in random order. Eighteen test subjects were involved altogether.
An intermediate analysis of the results showed that 3 test subjects were not capable of delivering sufficiently systematic pitch judgments. Their results were therefore excluded from those brought together for the final analysis. Also it became clear that the pitch distributions of the three different types of sound sample were not significantly different from one another (for this see [13]). Therefore the results were amalgamated, in order to increase the statistical significance of the distributions. Each pitch distribution is therefore based on 147 individual comparisons.
Fig. 2 shows as examples the pitch distributions of bells 14, 9 and 8. Bell 14 has a partial tone structure quite close to the ideal arrangement. Bell 9 is also melodious, though it deviates considerably from the ideal because the fourth, sixth and seventh partial tones are absent. The partial tones of bell 8 were not arranged according to any meaningful pattern; their strike pitch proved to be particularly ambiguous. The relative frequency density (the ordinate in Fig. 2) is the proportion of the total number of results (N=147) that fall into a particular frequency interval 0.2 frequency groups wide (the “integration interval”) [20]. The abscissa is the centre frequency of the integration interval. The frequency density functions arise as a result of the continuous shift of the integration interval along the abscissa. The width of the frequency groups and thus the integration interval are periodic in that the integration interval covers a fixed number of approximately ten evenly perceptible pitch differences [20 ]. As a result, almost co-incident frequency settings are aggregated, whereas significantly different pitches are shown separately.
The significance of the frequency densities was checked with a Chi-squared test by comparing with a random distribution of answers ranging across 15 frequency groups. The test gave a frequency density of 0.05 for a confidence level of 5% with N = 147. There is a high probability that those frequency density values which exceed this amount represent perception of an actual pitch, and the probability of mistake with higher frequency densities decreases rapidly. Therefore bell 14 has three, bell 9 at least four, and bell 8 at least six significant strike pitches (Fig. 2). Note that the distributions do not necessarily show all the audible pitches; this is not to be expected given the question posed to the test subjects and was also not the purpose of the experiment.
Since in general several maxima of different height occur in the distributions, all of which are significant in the above sense, the question arises as to what degree the frequency differences of the maxima concerned are significant. This was also estimated by means of a Chi-squared test; the significance of the differences between pairs of maxima was compared in each case against the proposition that if the total number of values allocated to them were constant, whether their heights would be the same in any population. It was inferred from this that the distributions of pitch values of the individual bells which are not significantly different from each other in the frequency density maxima, must in this sense be treated as equal. This means that, for example, the two biggest peaks for bell 14 are significantly different, so that one can speak of this bell as having a significantly dominant strike pitch (Fig. 2). On the other hand, for bell 9 the two highest maxima do not have a significantly different height. Therefore it is not possible to judge the order of significance of these two strike pitches; they must be regarded as equal. With bell 8 six strike pitches altogether appear equivalent in this sense.
The strike pitch can be quantified as the average value of all adjusted frequencies, indicated by a local maximum of the distribution, which fall into the window belonging to the maximum frequency density.
3.2. Vocal reproduction (reproduction experiment)
A method of post vocalisation was applied to the main group of 120 bells and as a check additionally on five bells of the aforementioned sub-group. The test subject was in an sound-isolated measurement room and could play a tape recording of the test sound by pushing a button (the whole sound, that is a sound segment consisting of the first three seconds after the impact; peak value of the volume was 70 dB; playback used DT48 binaural free field equalized headphones). The test subject was asked to reproduce the spontaneously perceived strike pitch of the test sound immediately afterwards by humming or singing it. Repeating the test sound was not allowed, in order to encourage a spontaneous impression of the pitch and to avoid analytic hearing if possible. Then the next test sound stored in random order on the test tape could be recalled, and so on. The tones reproduced by the test subjects were recorded with a microphone on another tape and analysed later by the test manager. The analysis involved the aural determination of the pitch-equivalent frequency of a pure tone by the test manager. This procedure was preferred to the direct “objective” measurement of the basic frequency of the hummed tones, because the accuracy and reliability possible for basic frequency measurement of the natural voice is rather less than the performance of an experienced listener. Additionally it emerged from the experiments that some test subjects did not immediately hit the exact pitch desired, but hummed a sliding tone which reached the final value desired only after a little time. The test manager could easily take this into account in the aural determination of the pitch-equivalent frequency and therefore get reliable results without too much work. The main advantage of the reproduction method which was crucial for these investigations is its saving of time as well as in the fact that it facilitates spontaneous, realistic pitch specification by the test subjects. A disadvantage is that it relies on the ability of the test subjects to hum pitches, and that for determination of the pitch-equivalent frequency two successive hearing comparisons are necessary (one by the test subject, the other by the test manager), in contrast to the comparison method. Finally, a further restriction arises as a result of the limited vocal range of the test subjects. These disadvantages seemed unavoidable within the scope of the given possibilities and were accepted.
The test subjects were trained musicians, and because of the results of the adjustment test it was assumed that most of the strike pitches would lie within the vocal range of the test subjects. Nevertheless, it was considered that the exactness or universal validity of strike pitches determined in this way was subject to certain constraints. Therefore from the outset the objective was only to determine the musical note name of the strike pitch in terms of the normal temperament (A’ = 440 cycles per second). Consideration of the octave position was not attempted, i.e., all pitch judgments were transposed into the same octave. This is justified by the fact that for bells whose partial tone structure obeys the norm, the octave position in any case is usually in the region of the second partial tone (the Prime). However the results of the aural pitch determination show that octave ambiguity is almost the rule; the note name of the strike pitch is to a large extent unique, whereas there is a large uncertainty as to whether the octave position of the strike pitch is in the region of the Prime or the Hum. Eleven test subjects were involved. Nine of them did two pitch determinations for each bell, and the remaining two test subjects only one, so that for each bell altogether 20 pitch values were obtained. The results, i.e., the pitch-equivalent frequencies determined by the test manager, were represented in histograms in the same way as the results of the adjustment test.
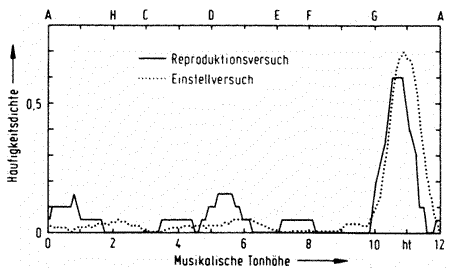
Fig. 3. Octave-normalised strike pitch distribution for bell 1. Ordinate: Frequency density as in Fig. 2, however refined with a window a semitone wide. Abscissa: Musical pitch, expressed by frequency measure interval, related to the frequency 2n 440Hz (n completely arbitrary). Increment of the half-tone window 0.1 semitones. Continuous curve: Reproduction experiment; dotted: Adjustment test.
Fig. 3 shows as an example the frequency density distribution of the octave normalized results for vocally reproduced strike pitches for bell 1 (the solid curve). The frequency density (ordinate) has a similar meaning to Fig. 2, but with an integration interval of 1 semitone = 100 cents in place of 0.2 frequency groups. To produce the distribution, the integration interval was shifted in steps of 10 cents along the abscissa. The musical pitch within the single-height octave is the frequency measure interval, related to the note representing A in normal temperament. In the same sense as discussed with the adjustment test (comparison method), it is to be assumed that a maximum in the frequency density distribution forms the basis of perception of an appropriate pitch, if the height of the maximum exceeds a certain value. With the same method as before, but taking into account the test conditions (12 value classes; 20 judgments), for a probability of mistake of 1% a minimum value of the frequency density was found of 30%. A strike pitch at the appropriate value from the abscissa is inferred from each maximum which approximates to this value or exceeds it. The latter was objectively determined in the same way as explained at the end of section 3.1. Thus the results from the histogram in Fig. 3 for bell 1 show only one significant strike pitch with the value 10.71 semitones, or G# – 29 cents.
3.3. Comparison of the two methods
The reliability of the reproduction method was checked, because the strike pitches of the bells 1, 7, 9, 12 and 14 were determined by both methods. For comparison, all individual values of the adjustment test were converted into the same octave and displayed by means of the same integration interval as with the reproduction experiment (1 semitone) as a frequency density distribution. The dotted curve in Fig. 3 shows the result for bell 1. From the position of the major peak the strike pitch is determined as G# -13 cents. The largest difference between the strike pitches determined by both experiments had the value of 64 cents (for bell 14). The largest difference of the frequency densities of the dominant strike pitches was 13% (for bell 9). We conclude from this that it is indeed possible to determine the strike pitch categories reliably with the reproduction method.
4. Results
As the examples of pitch distributions in Fig. 2 and Fig. 3 make clear, it is not easy to present the results of either the aural or the algorithmic strike pitch determinations both concisely and without ambiguity. We try to solve this problem below, by concentrating on the overall question, which is the extent to which the dominant strike pitches determined by aural and algorithmic methods agree.
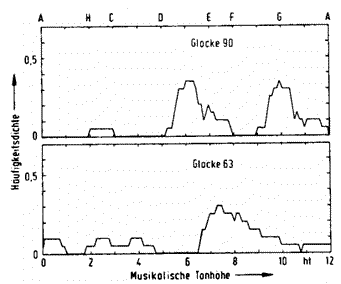
Fig. 4. Octave normalised strike pitch distributions from the reproduction experiment, displayed as Fig. 3. Bell 90 is typical of one with an ambiguous strike pitch, bell 63 has a strike pitch which is on the boundary of significance.
4.1. Aurally measured strike pitches
From the pitch distributions already presented for both the adjustment and the reproduction experiments it appears that the width of the maxima of the determined pitches is of the order of magnitude of a semitone. Fig. 4 shows two further distributions from the reproduction experiment, which are meant as examples of ambiguous strike pitches (bell 90), or of the significance boundary for a strike pitch (bell 63). We conclude from this data that it is not sensible to try to give reliable and representative values for the strike pitch to an accuracy of a few cents. The identification of the musical note name (that is, the “coarse tuning” with semitone accuracy) and the trend of possible divergence from normal temperament (that is, the “fine tuning”) is the best that is attainable. This does not exclude an individual experienced observer obtaining a higher accuracy of reproducible pitch determinations. Because of the considerable differences in pitch sensation between different individuals, such measurements are only of limited importance.
A summary of the results of the reproduction experiment with all 137 bells (including the results of those 12 bells, which were taken only in the adjustment test, correspondingly converted and included) is given by the following figures – note that all pitch values taken in this experiment are octave normalised:
- 97% of the bells have at least one significant strike pitch
- 69% of the bells have a single dominant strike pitch.
- across all 137 bells no significant preference for any strike pitch shows up within the normalized octave; the strike pitches are evenly distributed.
Table I.
Aurally measured, or algorithmically calculated pitch-equivalent frequencies (in cycles per second) of 17 bells (adjustment test; 15 test subjects; 147 adjustments), in each case in the reverse order of their frequency density or its calculated weight. The strike pitches listed are, for the aural measurements strike pitches, only those with equal high importance, and for the algorithmically determined, only the most significant ones (see text).
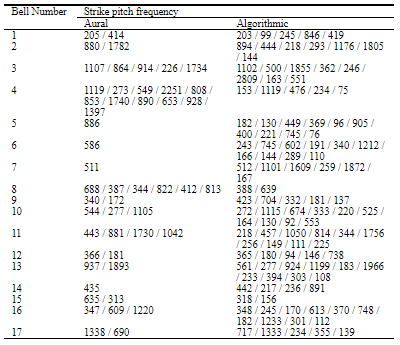
Further conclusions are available from the results of the adjustment test. Table I shows the equivalent frequencies (in cycles per second) of the aurally measured strike pitch for each of the 17 bells, in the reverse order of the appropriate frequency densities, i.e., in the order of rank of their importance. Only the most significant pitches in the sense of the definitions indicated in paragraph 3.1 are listed. It is clear the indicated rank orders are not very reliable. Only with bells 5, 6, 7 and 14 one can speak of a significantly dominant strike pitch. Bells 1, 2, 9, 10, 12, 13, 15 and 17 either have two strike pitches or have an ambiguous octave position. Octave ambiguity must obviously be regarded as a more or less typical characteristic of the strike pitch. Taking this into account, one can then say that 12 of the 17 bells, i.e. 71%, possess only one significantly dominant octave normalised strike pitch. The good agreement of this value with the appropriate percentage of all 137 bells given previously suggests that this sub-group of 17 bells is largely typical of the whole. The proportion of historical bells, whose strike pitches are ambiguous regarding their musical note name, can therefore reliably be stated as approximately 30%.
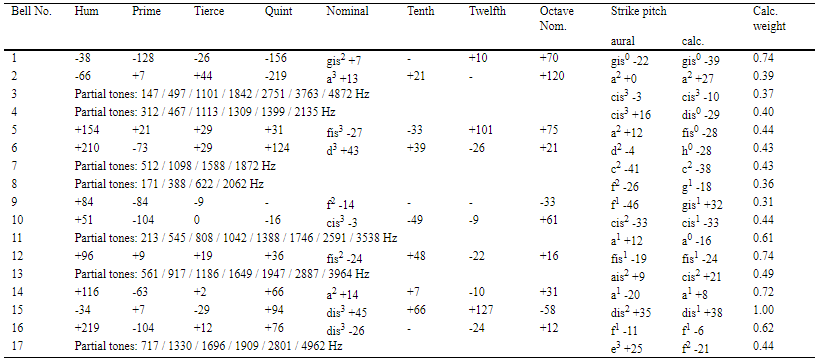
Bearing in mind the limits described to measurement accuracy and octave ambiguity, it is appropriate to classify the strike pitches according to three criteria: note name, fine tuning and octave position, particularly since this corresponds to a large extent to normal practice. In this way each of these three aspects can be separately discussed. In Table II an appropriate representation method is used. As far as possible, the partial tones of the 17 bells were arranged as in Fig. 1, where the Nominal frequency served as reference value. The tuning of the remaining partial tones is described by their deviation in cents from the ideal value referred to the Nominal. So, for example, if the Prime tone had exactly half the frequency of the Nominal, it would appear in Table II with a deviation of 0 cents. The absolute height of the Nominal is indicated by its note name, octave position and fine tuning related to normal temperament (A’ = 440 cycles per second). For example the Nominal indicated for bell 1 is gis2 + 7 (7 cents positive deviation from the two-primed G#), which is a frequency of 834 cycles per second. For those bells whose partial tones could not be conveniently fitted into the pattern, the partial frequencies are listed for those partial tones which were reasonable audible, i.e. those with positive level surplus. Also listed in Table II are those strike pitches from Table I ranked first in order of significance (either aurally measured, or calculated), again related to normal temperament. For instance, the designation gis0 – 22 for bell 1 in Table II corresponds to the frequency of 205 hertz in Table 1.
The figures show that the tuning of the partial tones throughout is quite inaccurate compared with the ideal. Furthermore, they suggest the tendency already mentioned that the fine tuning of the strike pitches corresponds better with that of the Nominals than with the Prime. In order to verify this quantitatively, those bells from Table II are considered for which the note name of the strike pitch corresponds with that of the Nominals. The average value of the deviations between the fine tuning of the aurally determined strike pitch and the Nominals amounts in these bells to 25 cents, whereas it is 40 cents compared with the Prime. Additionally, clear trends show up concerning the direction of the deviations. They can be described by the arithmetic average values of the appropriate tuning differences. These same amount to – 24 cents compared with the Nominals and + 30 cents compared with the Prime. That is, the strike pitch is on the average somewhat flatter than the octave-displaced Nominal, and sharper than the Prime. The letter tendency was already clear from the discussion in section 2 about Fig. 1.
As regards the octave position of the strike pitch, it appears that with those bells whose partial tones follow the standard pattern, there is a pronounced tendency of the strike pitch to fall in the area of the Prime; often, however, equivalent strike pitches occur in the region of the Hum. This is remarkable, when with bells with standard partial tone structure, strike pitches in the area of the Hum are usually not considered.
Table II.
Summary of frequencies or pitches with note name, octave position and fine tuning, for the sub-group of 17 bells (as in Table 1). All fine intonation values in cents in columns 2 to 5 and 7 to 9: deviations of the partial frequencies from the norm; reference value is frequency of the Nominals. Column 6: absolute tuning of the Nominal, relative to normal temperament. Columns 10 to 12: aurally or algorithmically determined strike pitch (relative to normal temperament) and weights of the latter. The strike pitches in each case are those listed first in Table I. If the partial tones are not in the normal arrangement, their frequencies are given.
4.2. Algorithmically determined strike pitches
In Table I the calculated equivalent frequencies of the strike pitches in the third column are specified in the reverse order of their calculated weight, i.e. in the order of rank of their importance. Only the significant pitches were considered, i.e., those whose weight is at least half of the maximum weight or a value of 0.2 (this limit is arbitrary; it was chosen for clarity).
In comparing the algorithmically calculated and aurally measured strike pitches, again three aspects were considered; note name (coarse tuning with semi-tone accuracy), fine tuning (deviation from normal temperament within the note name) and octave position. In this way we can more easily take into account the basic statistical character of both the algorithmic and the aural pitch determinations. An analysis of the data from the adjustment test in Table I, performed in this way, results in the following:
- the first calculated strike pitch agrees both in octave position and note name with the first aurally measured pitch in seven bells, i.e. 41 %.
- the first calculated strike pitch agrees both in octave position and note name with any of the equivalent aurally measured pitches in eleven bells, i.e. 65%.
- the first two calculated strike pitches agree both in octave position and note name with two of the equivalently aurally measured pitches in 13 bells, i.e. 76%.
- the first calculated strike pitch agrees with the note name (but not necessarily the octave position) of the first aurally measured pitch in 10 bells, i.e. 59%, (see Table II).
- the first calculated strike pitch agrees in note name only with any of the equivalent aurally measured pitches in 12 bells, i.e. 71%.
- in the last group specified the octave position but not the note name also corresponds in 11 of 12 cases (92%).
In order to measure the statistical significance of the algorithmic note name determination even more reliably, the results of the reproduction experiment can be considered. This results in the following:
- the first calculated strike pitch agrees with the note name with the first aurally measured pitch in 79% of the bells.
- for 84 of 95 bells (88%) with only one dominant octave-normalised strike pitch, this pitch agrees in note name with the first calculated pitch.
- the first-ranked aurally measured strike pitch agrees in note name with one of the first two, three, or four calculated strike pitches in 86%, 97%, or 99% of the bells.
In view of the fact that a substantial number of the historical church-bells had only moderate tone quality and almost indefinable strike pitches, one would not expect the close relationship between algorithmic and aurally determined strike pitches demonstrated by the average values above. On the other hand, for bells with well-pronounced strike pitches a higher measure of agreement could be expected. The weight of the calculated strike pitch is a suitable basis for discrimination. The last column in Table II gives examples of this. Compared with the pitch weight of “natural” complex tones the values are quite small, which shows how weakly pronounced the strike pitches of the bells concerned are. For example, a harmonic complex tone with 10 harmonics and a fundamental frequency of 300 cycles per second has a weight for the basic pitch of 2.7. It can be assumed that above a certain weight the strike pitch is unique and so pronounced that an almost certain prediction (at least as regards note name) can be made. A better determination of this limit value can be made from the average value of the weights of the correctly calculated strike pitches. For example, the average value of those weights in Table II for note names for which algorithmically and aurally determined values agree, is 0.61. The similar value from the reproduction experiment with 137 bells is 0.62. It is therefore a good assumption that strike pitches with calculated weights over approximately 0.6 are reasonably predictable. Indeed, one finds in Table II that for those six bells whose calculated pitch weight is larger than 0.6, the calculated and aurally determined note names correspond without exception. From all 137 bells the calculated pitch weight is larger than 0.6 in 64 cases (47%); again, for these bells the algorithmically and aurally determined note names correspond without exception.
It is a good assumption that the weights of the calculated strike pitches should be in close relationship with the frequency density determined in the aural test for the pitches concerned. If one correlates these two measures for all pitches from Table I, matching within a semitone, then indeed a relationship is found significant at the 99.9% level (r=0.597; N = 40). Nevertheless this relationship must be regarded as relatively loose, because for example the frequency densities concerned are relatively high for bells 5, 6 and 9 and the dominant (aural) strike pitches are to a large extent unique, while the appropriate calculated weights are situated below the average and the note names determined aurally or algorithmically do not correspond (see Tables I and II). A hearing calibration experiment showed that the significance of the strike pitches of these three bells is far smaller than is at first suggested by the height of the appropriate maxima in the pitch histogram. We infer from this result that from the clarity and frequency with which a strike pitch is dominant in the hearing experiment, cannot be related directly to its calculated significance, although a certain connection of the two measures exists. Looked at another way, the reliability with which a dominant strike pitch can be determined algorithmically is related to its significance, and the calculated weight seems to be a useful measure for this.
The following analysis will show conclusively to what extent, beyond the note name and the octave position, the tendencies of the fine tuning are also algorithmically assignable. In Table II are 10 bells for which the calculated and aurally determined strike pitches have corresponding note names.
The appropriate fine tuning does indeed show a correlation, which is significant at the 99%-level (r=0.764). The average value or the standard deviation of the differences between calculated and aural tuning differences amounts to 0.9 cents or 17.3 cents. With N = 10 this gives a confidence interval between -11.5 cents and + 13.3 cents. Therefore one can state the average accuracy of the algorithmically determined fine tuning as approximately plus/minus 15 cent. The findings are confirmed by consideration of the relationship between the fine tuning of the strike pitches and those of Nominal or Prime tone, as described in the preceding paragraph for the aurally determined strike pitches. The average values of the deviations between calculated strike pitches on the one hand, and Nominal or Prime tones on the other hand, are 15 cents or 38 cents. The algorithmically calculated strike pitch has therefore a closer relationship regarding its fine tuning with the Nominal as compared to the Prime tone, as was found before for the aurally measured strike pitch. Furthermore, the averages of the divergences also agree with the directions of the divergences established in the previous section: the arithmetic average value of the tuning discrepancy between calculated strike pitch and Nominal is -11 cent, while the same value relative to the Prime tone is +25 cent.
The results of the algorithmic strike pitch determination can be summarised as follows:
- For historical church bells of the type examined, the algorithmically determined note name ascertained from the weightiest calculated pitch agrees with the note name of the highest-rated aurally determined strike pitch in 79% of the cases. For bells which have a significantly dominant strike pitch, this agreement is observed in 88% of the cases. The algorithmic note name determination proves 100% reliable for those bells whose calculated pitch weight exceeds the value 0.6; the proportion of such bells was 47%.
- For those bells, whose strike pitch note name was correctly determined by the algorithmic procedure, the octave position of the strike pitch is correctly indicated by the weightiest calculated pitch with a probability of 90 to 100%. This means that where the aurally assessed octave position is clear, it is identical with the objectively ascertained ones, and if the aurally determined octave position is ambiguous, one of the two octave positions is given algorithmically.
- For those bells whose strike pitch note names are correctly determined by the algorithmic procedure, the fine tuning determined by the weightiest calculated pitch agrees reliably with the direction of the tuning deviation within the note name. The average accuracy of algorithmic determination of the fine tuning is approximately plus/minus 15 cents.
5. Final Conclusions
As described initially, the pitch sensation caused by a bell sound is basically ambiguous. From our aural pitch determinations it follows that, even if the test subjects are asked for the dominant strike pitch the responses never concentrate on only one pitch. Bells that possess a pronounced strike pitch can be assigned a musical note name which is unique, but the same cannot be said of their octave position. With many melodious bells it cannot be decided clearly whether the strike pitch is situated in the region of the Prime or the Hum.
The strike pitch determination rates regarding note name, octave position and fine tuning obtained with the algorithmic procedure, are so high that one could hardly expect a better agreement in view of the typically moderate sound quality of the examined bells and the limits of accuracy and significance attainable during the aural pitch determination. This does not preclude further improvements in the pitch computation method. However, we did not succeed in deriving criteria for improvements from the results described here. From the fact that the procedure and thus the psycho-acoustical concepts of pitch perception on which it was based worked to a considerable degree during the algorithmic strike pitch determination, we conclude the fact that – as initially stated – the “strike pitch mystery” can be regarded today as being to a large extent solved.
Concerning the practical solution of the problem, to determine the strike pitch of a bell algorithmically (which does not always give a clear determination), then we derive from the results described the following simple procedures.
One subjects the sound signal to the pitch analysis procedure of Terhardt et al. [18] and selects the pitch with the highest weight. If the weight exceeds the value 0.6, then it is practically certain to be the strike pitch. If the weight is below 0.6, then one can expect a high correlation with the aurally determined pitches, however a definite prediction of the strike pitch is not possible. In this case it is appropriate to take into consideration not just the pitch with greatest but also those with lesser weight. The complete set gives a good picture of the weaker strike pitches competing with each other. However, reliable statements about their order of rank are not possible.
We thank Dr. T. Breuer and Dr. M. Nitz for crucial suggestions for these investigations, as well as Dipl.-Ing. G. Stoll and Dipl.-Ing. W. Aures for advice and energetic support. This work was sponsored by the special research area 204 “Hearing” of the German Research Council.
(Received on 23 June 1983.)
[1] Arts, J., The sound of bells. J. Acoust. Soc. Amer. 9 [1938], 344.
[2] Fehn, T., Die Gliederung des Tonaufbaus in ihrer Bedeutung für die Klangqualität der Glocke. In: Beiträge zur Glockenkunde, hrsg. v. Beratungsausschuß für das Deutsche Glockenwesen, Heidelberg 1970.
[3] Griesbacher, P., Glockenmusic. Regensburg 1927 and 1929.
[4] Jones, A. T., The strike note of bells. J. Acoust. Soc. Amer. 1 [1930], 373.
[5] Jones, A. T., The effect of temperature on the pitch of a bell. J. Acoust. Soc. Amer. 1 [1930], 382.
[6] Jones, A. T. and Alderman, G. W., Further studies of the strike note of bells. J. Acoust. Soc. Amer. 3 [1931/32], 297.
[7] Meyer, E. und Klaes, J., Über den Schlagton von Glocken. Die Naturwissenschaften 21 [1933], 697.
[8] Plomp, R., Pitch of complex tones. J. Acoust. Soc. Amer. 41 [1967], 1526.
[9] Plomp, R., Aspects of tone sensation. Academic press, London 1976.
[10] Ritsma, R., Frequencies dominant in the perception of the pitch of complex sounds. J. Acoust. Soc. Amer. 42 [1967], 191.
[11] Schaeben, J., Glocken, Geläute, Türme im ehemaligen Landkreis Euskirchen. Rheinland-Verlag, Köln 1977.
[12] Schouten, J. F., The perception of pitch. Philips Techn. Review 5 [1940], 286.
[13] Seewann, M. und Terhardt, E., Messungen der wahrgenommenen Tonhöhe von Glocken. In: Fortschritte der Akustik, VDE-Verlag, Berlin 1980, pp. 635-638.
[14] Stüber, C. und Kallenbach, W., Akustische Eigenschaften von Glocken. Physikal. Blätter 5 [1949], 268.
[15] Terhardt, E., Zur Tonhöhenwahrnehmung von Klängen. Teil I, Acustica 26 [1972], 173; Teil II, Acustica 26 [1972], 187.
[16] Terhardt, E., Calculating virtual pitch. Hearing Research 1 [1979], 155.
[17] Terhardt, E., Die psychoakustischen Grundlagen der musikalischen Akkordgrundtöne und deren algorithmische Bestimmung. In: Tiefenstruktur der Musik, Techn. Universität Berlin 1982, pp. 23 – 50.
[18] Terhardt, E., Stoll, G. und Seewann, M., Algorithm for extraction of pitch and pitch salience from complex tonal signals. J. Acoust. Sec. Amer. 71 [1982], 679.
[19] Weissenbäck, A. und Pfundner, J., Tönendes Erz. Verlag Hermann Böhlaus, Graz-Köln 1961.
[20] Zwicker, E., Psychoakustik. Springer, Heidelberg 1982.