I have always used the interval between octave nominal and nominal as a measure of the relative weight and thickness of a bell, because of the octave nominal’s influence on strike pitch. Bells which are proportionately thicker and heavier have flatter octave nominals.
In a discussion in August 2022, Ben Kipling of Matthew Higby and Company suggested that diameter * nominal frequency was a measure for scale of thickness, and suggested looking at how the interval between prime and nominal was related to scale of thickness. In fact, a metric of this type was first proposed by André Lehr in his 1986 paper Partial groups in the bell sound (ref 1). In this paper, he uses radius * hum as a metric of thickness. This metric was used by PJM Roozen-Kroon in her work using computer simulation to design bells, including major third bells (ref 2).
This investigation uses information from 7,737 bells to investigate how the octave nominal tuning and prime tuning depend on the diameter (or radius), hum and nominal frequencies.
Models to be investigated
In this investigation, all logarithms are natural logarithms to base e – excel function log(). All diameters are in metres, and all frequencies in Hz (cycles per second).
The prime interval to nominal in cents is:
1731.234 * log (prime frequency / nominal frequency)
and the octave nominal interval is:
1731.234 * log (octave nominal frequency / nominal frequency).
In the investigation I wanted to assess the relative contribution of diameter and nominal or hum frequency, which suggests a logarithmic approach. The simplest models relating the prime to diameter and nominal or hum frequency are:
prime cents = b0 + b1 * log(diameter * nominal)
prime cents = b0 + b1 * log(diameter * hum)
and the equivalent models for octave nominal are:
octave nominal cents = b0 + b1 * log(diameter * nominal)
octave nominal cents = b0 + b1 * log(diameter * hum)
Models allowing for different contributions from diameter and nominal or hum are:
prime cents = b2 + b3 * log(diameter) + b4 * log(nominal)
prime cents = b2 + b3 * log(diameter) + b4 * log(hum)
and the equivalent models for octave nominal are:
octave nominal cents = b2 + b3 * log(diameter) + b4 * log(nominal)
octave nominal cents = b2 + b3 * log(diameter) + b4 * log(hum)
However, because of the two independent variables in these models, they are harder to show on a graph.
A model using nominal frequency rather than hum frequency is more convenient in practice, if it is adequate, because information on the nominals of bells is more readily available (e.g. in Dove’s Guide).
All bells including true-harmonic
In my database I have 7,737 bells which have a diameter and partial frequencies for hum, prime, nominal and octave nominal. These bells are from many countries, founders and dates. Here are plots of prime cents against log(diameter * nominal), prime cents against log(diameter * hum), octave nominal cents against log(diameter * nominal), and octave nominal cents against log(diameter * hum):
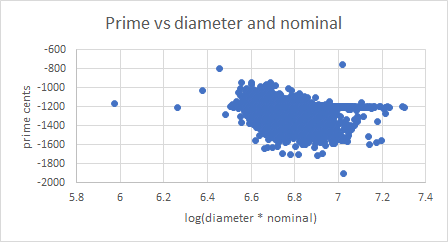
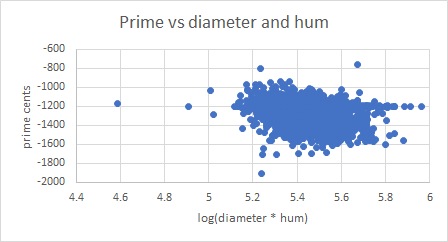
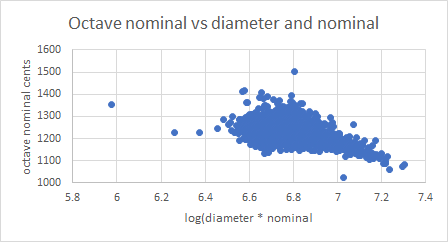
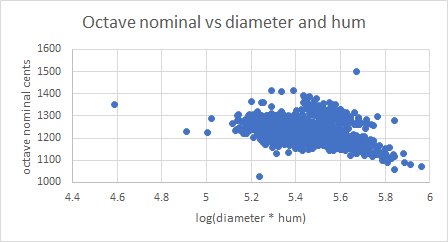
The outlier on the left of all the plots is a bell dated 1615 by Van Den Ghein, featured by André Lehr in his 1986 paper (ref 1). Removing this bell from the investigation made no material difference to the results.
The bells with octave primes are clearly visible in the first two plots. This shows what we already know, that bells with different scales of thickness can have octave primes, due to detailed differences in the design of each bell.
The correlation coefficients are:
Primes against diameter * nominal: 0.290
Octave nominals against diameter * nominal: 0.515
Primes against diameter * hum: 0.371
Octave nominals against diameter * hum: 0.508
Perfect correlation between the variables (straight line graphs with no scatter of points around the line) would have correlation coefficients of 1.0. So the primes are moderately correlated with diameter * nominal and diameter * hum. The correlation of octave nominals with diameter * nominal and diameter * hum is stronger, but still not very strong.
A regression analysis of the more complex models, with separate coefficients for diameter and nominal or diameter and hum, shows that in all cases there is no statistical significance between the coefficients of diameter and nominal or diameter and hum, so that the simpler model is adequate.
For these bells, the strongest correlation is that between octave nominals and diameter * nominal, so that it is appropriate to use nominals (on which data is more often available) to indicate scale of thickness. The importance of the octave nominal is its influence on the strike note of a bell.
The stronger correlation of the primes with diameter * hum rather than diameter * nominal is no doubt because many of these bells are not true-harmonic, and in such bells flat primes often imply sharp hums, i.e. there is correlation between the two partials.
Bells without octave hums or primes
The octave primes and hums clearly affect the models. If all bells with a prime interval between -1210 cents and -1190 cents or hums between -2410 and -2390 cents are removed, 4,139 bells remain. Here are the plots for the remaining bells:
For this reduced set of bells, the correlation coefficients are:
Primes against diameter * nominal: 0.510
Octave nominals against diameter * nominal: 0.383
Primes against diameter * hum: 0.439
Octave nominals against diameter * hum: 0.385
So the prime correlation is rather better, as expected the octave primes were affecting the previous result. The octave nominal correlation has got worse. My interpretation is that having removed 3,598 bells with a more controlled design giving octave primes and hums, the remaining bells without octave primes have a wider variation in design which affects the octave nominal.
As for the full set of bells, with this reduced set the model coefficients for diameter and nominal or diameter and hum separately have very similar values, with a difference which is not statistically significant. So again the simple model using diameter * nominal or diameter * hum is adequate.
Primes and Octave Nominals
The above analysis shows that the prime interval and the octave nominal interval are moderately well correlated to diameter * nominal. The final question is, are they correlated with each other? Here is a plot, for all 7,737 bells:
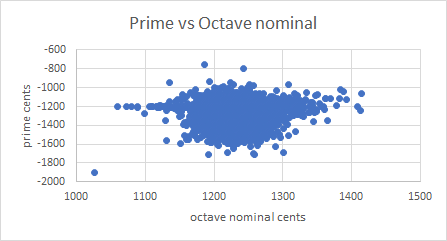
The horizontal line for octave primes can be see, but there is no evident correlation. The statistics confirm this, the correlation coefficient is 0.089 which confirms there is no relationship between the quantities. This is explicable by considering what parts of the bell affect the two partials. Here are plots showing how the two partials are stimulated at various points from rim to shoulder, produced using the new experimental technique for partial identification. The x-axis in these plots is relative distance from lip to shoulder, with the lip on the left:
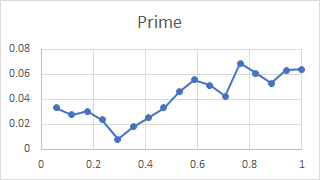
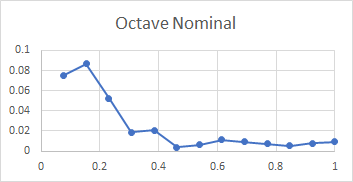
The prime is most stimulated by striking the bell from half way up to the shoulder. The octave nominal is most stimulated when the bell is struck near the rim. So the relative thickness / weight of a bell at different points between lip and shoulder affects these two partials in very different ways.
Conclusion
If diameter * nominal is a measure of scale of thickness, there is a moderate correlation with prime tuning: bells which are proportionately thicker and heavier have flatter primes. The bell designer and tuner has considerable influence over this and can produce bells with octave primes for any realistic scale of thickness.
For all bells, the octave nominal tuning has a better correlation with diameter * nominal, though when bells with octave primes are removed, the correlation is not as good.
The alternative model suggested in (ref 1) and (ref 2) of using diameter * hum as a measure of scale of thickness, is also valid, but produces no better results. The choice of which to use is a matter of convenience depending on what data is available.
The relative contribution of diameter and nominal, or diameter and hum, to the models are the same to within statistical limits and so there is no need to use a more complex model with different factors for the two values.
Though both partials are moderately well correlated with diameter * nominal and diameter * hum, they are not at all correlated with each other.
References
- Lehr, André, Partial groups in the bell sound, Journal of the Acoustical Society of America, 79 (6), June 1986
- Roozen-Kroon PJM, Structural optimization of bells (PhD Thesis), Technische Universiteit Eindhoven, 1992