This page was re-written on 15/8/2022 to describe tests on three bells and an expanded procedure. Since this re-write, the technique has been successfully applied to twelve bells with a range of dates and founders, some with archaic profiles.
This page describes work carried out in July and August 2022 on identification of bell partials. In a bell of conventional shape, the lowest five partials (hum, prime, tierce, quint and nominal) are always in the same order when ranked by frequency, and almost always have intervals between them that lie in a defined range. Wavanal uses this information to assign partial names when analysing a bell recording. It uses the relationships between upper rim partial frequencies described here to assign the names of the upper partials.
For bells of unconventional shape, such as long-waisted bells, these rules may not hold and the lowest partials may not be in the conventional order of frequency. A way was needed to identify the partials in these bells.
In tubular bells, the partials have a completely different arrangement, and these bells are excluded from this investigation.
There are two different ways to think about assignment of partial names, especially for the nominal:
- a functional view, where the nominal is the partial that determines the note-name of the bell. In this view, the nominal can be identified by establishing the strike pitch of the bell. This was the approach used when identifying the nominals of tubular bells. This approach fails when the bell pitches by a partial other than the nominal, such as very small bells which pitch by the hum, and very big bells which pitch by an upper partial
- a mode-of-vibration view, where the nominal is the partial with an antinode at the soundbow, with 8 nodes around the perimeter of the bell. This is the view which is investigated in this experiment.
As well as finding a way to confirm the identification of partials in long-waisted bells, another goal of this work was to find a way to identify the set of three partials between nominal and octave nominal.
Partial modes of vibration
This subject is covered in detail in my PhD thesis (1)on pages 87 onwards.
Each partial or mode of vibration in a bell has nodes and antinodes across the body of the bell. Nodes are points which have no movement in the direction of vibration, anti-nodes are points of maximum amplitude. The nodes lie in lines from the rim to the crown of the bell, and in circles around the bell parallel to the rim. The so-called rim partials are the partials with an antinode, a circle of maximum vibration amplitude at or near the soundbow. These partials are maximally stimulated by the blow of the clapper and the rim partials from nominal upwards create the strike note. Other partials, including those in groups II and III listed for this bell, have a nodal circle in the soundbow. All the modes of vibration have nodal lines from soundbow to crown.
As an illustration of nodal lines and nodal circles, here is the mode of vibration of a bell’s tierce:
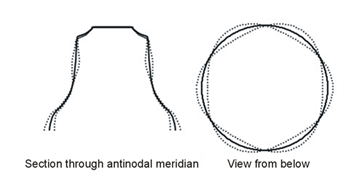
This mode vibrates strongly at the rim, i.e. has an antinodal circle at the rim, and has a nodal circle (a circle of least vibration) about half way up the bell. The mode has six nodes and six antinodes around the rim. The nodal lines (the lines of least vibration) stretch up the bell from lip to shoulder.
The number of nodal lines from rim to shoulder is always even. The vibrations either side of a nodal line on the rim, i.e. a stationary point in the right-hand diagram above, are in anti-phase. So in this diagram, at an instant in the vibration, if one sector is flexed away from the centre of the bell, adjacent sectors must be flexed towards the centre of the bell. The only way this is mechanically possible is if the number of sectors is even. A mathematical analysis of this is given in Perrin and Charnley’s paper Group Theory and the Bell (3).
If it is possible to determine the number of nodal lines for a mode of vibration, this information can be used to help identify partials, and resolve identification ambiguities between partials.
If a bell is not exactly circular, each mode of vibration splits into two modes called doublets, with a slightly different frequency. A demonstration of why this occurs is given here.
The positions of the nodal lines of one half of the doublet for an individual partial coincide with the anti-nodal lines of the other half of the doublet, and vice-versa. The positions of the nodal and anti-nodal lines are fixed by the physical shape of the bell and the deviation from exact circularity. When a bell is struck on its soundbow, if the strike point is on a nodal line of a doublet for a particular partial, that half of the doublet will be at its quietest and its pair will be at its loudest. When struck midway between the nodes of a doublet pair, both halves of the doublet will sound. Doublets prove to be the key to determining the number of nodal lines.
Nodal circles up the bell from lip to shoulder were also investigated, by looking at how different partials are stimulated when striking the bell at several points between lip and shoulder.
Main partials investigated in the experiments
The partials investigated, which include those primarily responsible for the musical quality of a bell, were as follows. The position of the nodal circles is given as the fraction of the distance from lip to shoulder:
| Partial | Interval to nominal | Type of partial | Nodal lines | Position of nodal circles |
| Hum | Two octaves below | Rim | 4 | |
| Prime | Octave below | Group II | 4 | 0.30 |
| Tierce | Major 6th below (minor 3rd above strike) | Rim | 6 | 0.54 |
| Quint | 4th below (5th above strike) | 6 | 0.19 | |
| Nominal | – | Rim | 8 | 0.54 |
| II-4 | 8 | 0.19 | ||
| III-3 | 6 | 0.20, 0.48 | ||
| III-2 | 4 | 0.19, 0.52 | ||
| Superquint | Roughly a fifth above | Rim | 10 | 0.54, 1.00 |
| Octave Nominal | Roughly an octave above | Rim | 12 | 0.28, 0.98 |
| I7 | Rim | 14 | 0.57, 1.00 | |
| I8 | Rim | 16 | 0.50 |
This information is taken from pages 94 and 95 of my PhD thesis (1), which pulls together information from André Lehr (2) and Perrin, Charnley and DePont (4). Full references are given below. The positions of the nodal circles are for the bell tested by Perrin, Charnley and DePont. Other bells may have them at different heights.
Bells used in the experiment
Three bells were used in this experiment, chosen to give a wide range of dates, founders and perceived bell quality.
| Bell | Founder | Date | Weight | Diameter | Nominal |
| Dorking service bell (5th of the previous peal) | John Wilnar | 1626 | 528kg | 0.99m | 832Hz |
| Dorking treble | Taylor | 1998 | 219.5kg | 0.64m | 1645Hz |
| Ranmore fourth | Mears & Stainbank | 1859 | 397.8kg | 0.89m | 952Hz |
Here are pictures of the three bells, marked up for the experiment as described in the next section.



The experiment is easier to carry out if there is good access all round the bell, to help both with marking it up, and to give space for the hammer swing.
Experimental procedure
The procedure used was adapted from Raleigh’s original investigation into bell partials written in 1890 (5). The principle is to strike the bell at multiple points around the rim, and identify, for each strike point and each partial, the relative intensity of each half of the doublet pair for that partial. Rayleigh’s original approach was adapted to take advantage of a laptop for frequency / amplitude measurement, and software for plotting the partials.
The rim of each bell was marked up with chalk to indicate the strike points. The partial investigated with the most nodal lines has 16 nodes and so we need at least 32 strike points and preferably many more. The bells were marked with between 54 and 76 equally-spaced strike points, the number chosen to give easy measurement. The marking does not need to be accurate, it was done with a steel tape. To avoid losing track of which strike point was which, each tenth strike point round the bell was marked with its number.
The bells were also marked with equally spaced strike points between lip and shoulder. The bells had between 13 and 22 strike points between lip and shoulder, the number again chosen to give easy measurement. To avoid the risk of knocking a piece out of the lip, the zeroth point (right on the lip) is not used.
The next step is to take a recording of the bell being struck at every one of the strike points around the rim, and each one of the strike points between lip and shoulder. Most recordings were taken on a laptop with microphone; one set was taken on a mobile phone. It is most important that the recorder does not distort or overload. If necessary, move the laptop or recorder further away until undistorted recordings result. Each blow should be roughly the same strength, and sufficiently heavy to stimulate the upper partials. It also helps if each blow around the rim is at the same height on the soundbow.
For the first recordings on the Dorking clock bell, a 1.5kg lump hammer was used, swung from about 5cm away. Subsequent recordings were taken with a 540g ball-peen hammer, using the ball to get an accurate position for each blow, again swung from about 5cm away. The analysis done on the recordings copes with minor differences in the heaviness of the blow. There is no perceivable difference between the results from the two different hammers.
At least 10 seconds must elapse between each blow, to allow for sufficiently accurate frequency analysis. Each set of recordings was done in one pass. To keep track of progress and to help with analysis of the recordings, I called out the number of every tenth position before making the blow.
Analysis of the recordings
The first step in the process is to split the recordings into individual sound files, one for each hammer blow. A naming scheme should be adopted to keep track of the large number of recordings.
My initial analysis of the recordings was done manually with Wavanal. This becomes very laborious due to the large amount of analysis required – measuring dozens of partials in hundreds of recordings, taking about a day per bell. I have now written software to automate the analysis, which produces identical results to the manual analysis. The manual procedure I originally used will be explained for one partial, because it gives a good insight into the physics involved.
The first step in the process is to determine the frequencies of each half of the doublet for each partial. The Interval (Hz) in Wavanal was set to 0.1Hz (which requires 10 seconds of sound). For some partials it was necessary to analyse several different recordings around the rim to identify both halves of a doublet.
In the Dorking service bell, the doublet pair for the nominal is 831.7Hz and 832.3Hz. So with the transform parameters in Wavanal set to Start Frequency: 825Hz, End Frequency: 840Hz and Interval: 0.1Hz the spectrum produced is as follows:
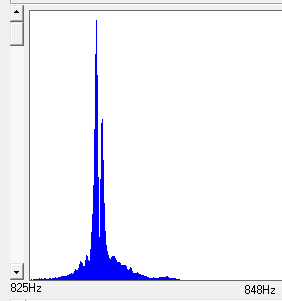
The two halves of the doublet can be seen. The amplitudes of both doublet frequencies were obtained by clicking on them and entering the amplitude values into a spreadsheet against the blow position of the recording. As the recordings are analysed, it becomes clear that amplitude shifts back and forth between the halves of the doublet as the blows proceed around the bell – sometimes one is stronger, sometimes the other.
Differences in the strength of the blow at each position will affect each half of the doublet equally, as they have the same pattern of vibration. So if alow is the amplitude of the lower frequency of the pair and ahigh the amplitude of the higher, the quantity alow / (alow + ahigh) gives the relative amplitude of the lower half of the doublet pair independent of the strength of the blow.
A plot of alow / (alow + ahigh) and ahigh / (alow + ahigh) against the position of the blow around the bell is as follows:
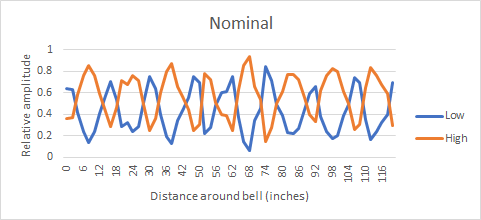
It is obvious from this plot how amplitude moves from one half of the doublet to the other as we proceed around the bell, moving between nodes and antinodes for each half of the pair. It is also clear that there are 8 node / antinode pairs around the rim, showing that this partial has been correctly identified as the nominal. This chart is cyclic: the position at the rightmost side is next to the leftmost. In fact the easiest way to visualise the pattern is to plot the same data for one half of the doublet as a polar plot against distance around the bell:

The pattern of eight nodes and antinodes becomes immediately obvious.
Once all the doublet pairs had been identified, the recordings from lip to shoulder were analysed. It becomes clear looking at the recordings that different halves of a doublet pair are stimulated differently at different points between rim and lip. This occurs both because it is unlikely that we will be hitting the bell consistently on a direct line from lip to shoulder, and also because the nodal lines for a partial may not follow a straight line from lip to shoulder, depending on the asymmetry in the bell. So the amplitude of both halves of each doublet pair was measured and then averaged.
To compensate for different strengths of hammer blow, the amplitudes for each strike point from lip to shoulder were normalised using the total amplitude for all the partials being investigated, at that strike point. This means that what is being measured is the relative amplitude of a partial against all partials investigated. If the relative amplitude of a partial at a strike point is large, either that partial is strongly stimulated at that point (possibly because the blow is on an antinodal circle for the partial), or all the other partials are not strongly stimulated at that point.
Here is the relative amplitude of the quint of Dorking treble plotted against relative distance from lip to shoulder:
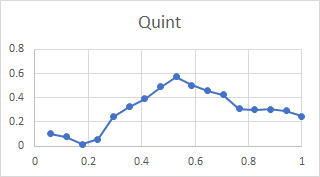
This shows the (relative) degree to which the quint partial is stimulated by blows at different points between lip and rim. It is obvious from this plot why the quint partial is very quiet in many bells – it is not much stimulated by blows near the rim.
Experiment results – nodes around the rim
Polar plots of nodal patterns around the rim for the three bells are very consistent. In every case, for the rim partials the pattern is very clear, leaving no doubt as to the number of nodal lines around the rim of the bell. For partials other than the rim partials there is generally a good pattern, but sometimes less clear, but the number of nodes around the rim can often be unambiguously determined. Despite the simplicity of the experimental procedure, it produces very good results. Here is a complete set of plots from the Dorking service bell:
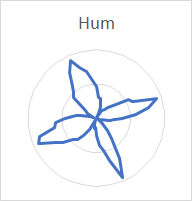
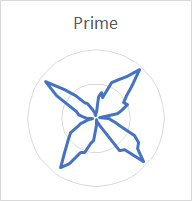
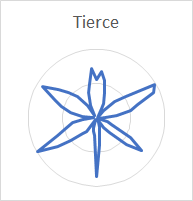
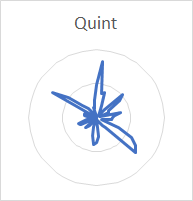

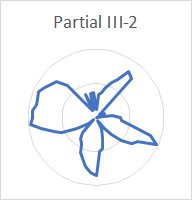
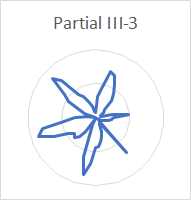
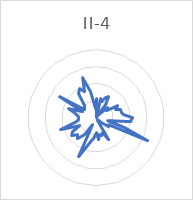

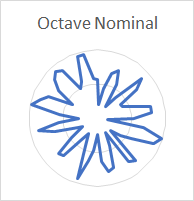
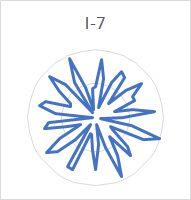

The increasing number of nodes for each succeeding rim partial (hum, tierce, nominal, superquint, octave nominal, I-7 and I-8) stands out clearly. The number of nodes for the prime, partial III-2 and partial III-3 is also clear. The nodes for the quint (6 in number) and partial II-4 (8 in number) are clear enough that they can be distinguished from the other partials, even though these two partials are very quiet and the analysis affected by noise.
As stated above, the plots for the other two bells provide equal clarity, with the exception of the quint in the Dorking treble. Despite detailed examination, no doublet could be detected for this partial, so no polar plot is possible.
Experimental results – from lip to shoulder
Here is a set of plots from lip to shoulder for all the above partials in the Dorking service bell. To recap, these plots show the relative amplitude of an individual partial compared with all the subject partials, for a hammer blow at a point between lip and shoulder. The x-axis of each plot is the relative distance of the hammer blow from the lip compared with the total distance from lip to shoulder, measured along the curve of the bell.
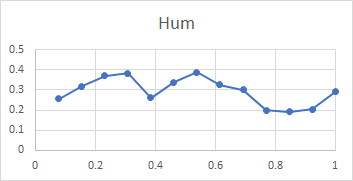
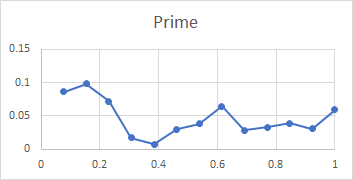
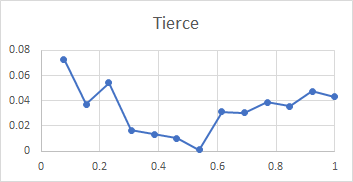
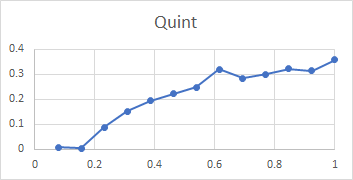
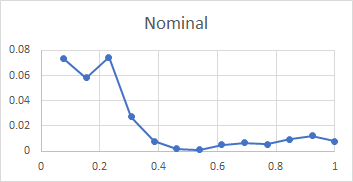
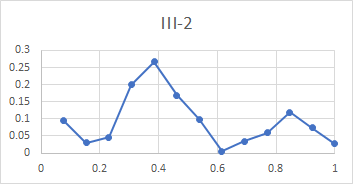
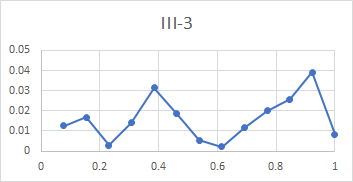
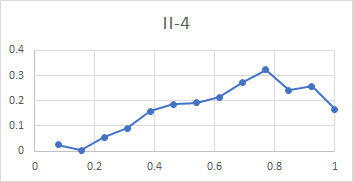
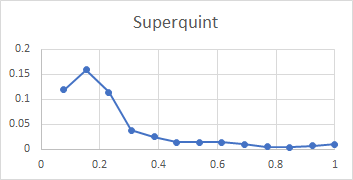
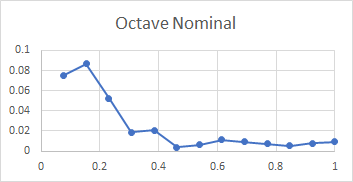
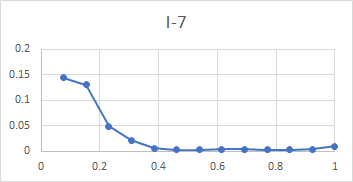
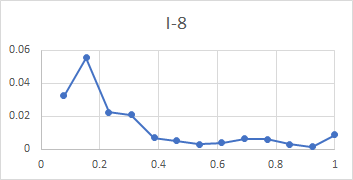
All three bells tested gave very similar plots, with the exception that the tierce and quint fell from mid-waist to soundbow in Dorking treble and Ranmore 4th, rather than rising as they do for this bell. It is clear from these plots that the rim partials other than the hum (tierce, nominal, superquint, octave nominal, I-7 and I-8) are maximally stimulated at or near the rim, which explains their prominence in spectra of bells stuck on the soundbow. The other partials (except the hum and prime) are quiet when the bell is struck on the soundbow, and are only strongly excited when the bell is hit higher in the waist.
The expectation is that these results will help distinguish rim partials from other partials in bells of unusual shape, where the partials are in a different order of frequency than in a bell of classic shape.
It is tempting to try to relate the form of these graphs to the positions of nodal circles given in the table above, and for the rim partials, there is some correspondence between minima in the plots and the nodal circle location. For other partials this is not practical, mainly because the plots show the relative strength of a partial compared to all the partials investigated, rather than some absolute measure of intensity for each individual partial. However, the consistency of the patterns across the three different bells encourages the hope that they can be used to help distinguish partials.
Comparison of the bells
It is not worth showing all the plots for the other bells as they are all very similar. Here for the sake of comparison are the polar and lip-to-shoulder plots for the nominals of all three bells:
- Dorking service

- Dorking treble

- Ranmore 4th

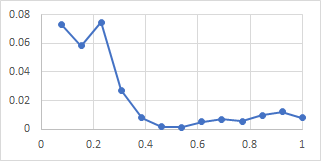
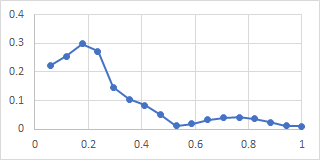
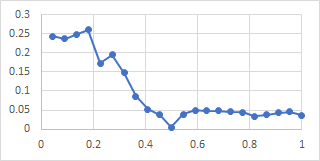
The polar plots show the six nodes, and the plots from lip to shoulder strongly suggest an antinodal circle half way up the bells, as found in the bell tested by Perrin, Charnley and DePont.
Conclusion
The results of these experiments are most satisfactory. Using only modest equipment (a tape measure and a hammer) it has proved possible to identify the vibration patterns of a significant number of bell partials. The procedure worked satisfactorily on three very different bells, and can be carried out on bells in the tower provided that access is possible all round the bell. The procedure copes well with variations of blow strength within a set of recordings. The success of the procedure gives hope that it can be used to identify partials in bells of unconventional shape, such as the long-waisted bells that prompted the investigation.
As a taster for the use of the procedure on other bells, it was used to investigate the long-waisted bell in Taylor’s museum, originally from Werrington, Northamptonshire. This bell has a partial just below the nominal that could be a sharp quint. However, this partial only has four nodes around the rim, and so cannot be the quint. It is possible that it could be partial III-2 with an unusually low frequency. Investigation continues!
References
1. Hibbert W. A., The Quantification of Strike Pitch and Pitch Shifts in Church Bells, PhD Thesis (2008)
2. Lehr A., Contemporary Dutch Bell-Founding Art, Neth. Acoust. Soc. Publ. No.7, 1965, pp. 20-49, reprinted in Rossing (6)
3. Perrin R., Charnley T., Group Theory and the Bell, Journal of Sound and Vibration, 31, pp411-418 (1973), reprinted in Rossing (6)
4. Perrin R., Charnley T., DePont J., Normal Modes of the Modern English Church Bell, Journal of Sound and Vibration, 90(1), pp29-49 (1983), reprinted in Rossing (6)
5. Lord Rayleigh, On Bells, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Fifth Series, Vol 29, No 176 (January 1890), reprinted in Rossing (6)
6. Rossing T. D., (editor), Acoustics of Bells, Van Nostrand Reinhold, (1984)