The first page in this series (What note do we hear when a bell rings?) explains briefly that the upper partials in bells have a significant influence on the note we hear and the general timbre of a bell. This article goes into more detail on the musical relationship between these partials.
The first figure shows a typical spectrum of a bell (the old 9th bell from St Mary le Tower, Ipswich):
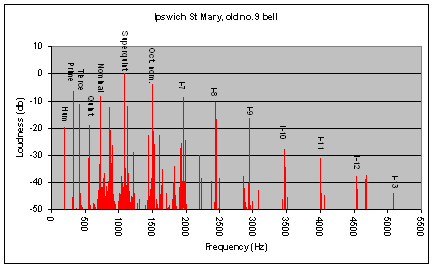
By upper partials, I mean the nominal, superquint, octave nominal and partials I-7 to I-13 visible above. These are prominent and roughly equally spaced in all bells. In thin, light bells these partials are spaced further apart. In thick, heavy bells they are closer together. These upper partials determine the strike pitch (the over-riding note of the bell), hence their importance. The first page explains that closely spaced upper partials flatten the strike note, and widely spaced upper partials sharpen it. These partials have an anti-node (i.e. a point of maximum amplitude of vibration) at the bell’s rim or sound-bow.
Various attempts have been made in the past to tune these partials, at least the lower ones, to exact musical intervals with the nominal. Investigation of over 8,000 bells shows that it is impossible to independently tune these partials or alter their frequencies by design changes in any bell of normal shape. The next figure shows the tuning of the significant partials of the bells investigated. The 8,071 bells include both bronze and steel bells, cover 9 centuries, 15 countries, more than 100 founders, and range in weight from 19 kg to 65 tonnes. The values plotted are the intervals of each partial to the nominal, expressed in cents or hundredths of a semitone.
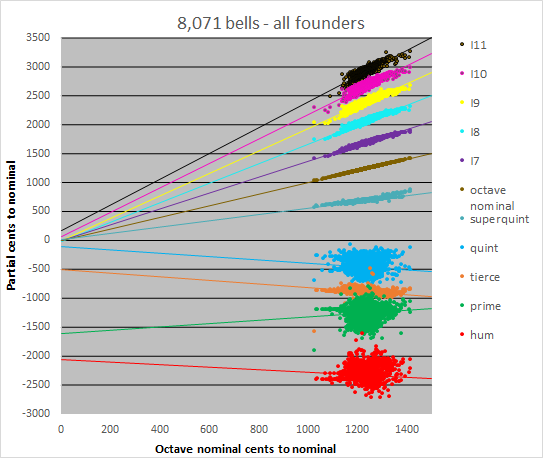
What this figure shows is that, for a particular octave nominal tuning, the intervals of all the upper partials are uniquely determined, with a linear relationship. The straight lines in the figure for each partial are regression fits to the data. The interval of the octave nominal relative to the nominal can be changed by tuning (typically, by thinning the bell in the region of the soundbow so the octave nominal sharpens, or skirting the bell so it flattens), but all the other upper partials move in exact proportion. This is not true for the hum, prime and quint, whose intervals to the nominal can be controlled by the bell founder independently of the octave nominal via design and work on the tuning machine, as can be seen by the scatter of values in the chart. Like the upper partials, the interval of the tierce to the nominal cannot be significantly changed on the tuning machine, though it can be influenced by careful design of the soundbow. Like the upper partials, the tierce also has an antinode at the soundbow.
The impossibility of independent tuning of the upper partials has not been recognised by bellfounders – in fact, some claim to tune them independently in big bells. An interesting case study in this regard is the Berlin Freedom bell, cast and tuned by Gillett and Johnston in 1950 and hung in the Rathaus Schöneberg in Berlin. A picture of this bell following its rehanging in 2001 (taken from the website of Ingenieurgruppe Bauen) follows:

Richard Offen, in a note to the Bell Historian’s Group, gives the background to the tuning of this bell: I well remember Wally Spragett telling me of his adventures tuning this bell. It was one of G & J’s early ventures into serious upper partial tuning … I seem to remember Wally saying that, because of the experiment, they made a bish of the tuning …, but as the bell was never to be rung with any other, they let it go – would have been a rather expensive mistake had the bell needed recasting like the Wanamaker Bell a few decades earlier! The bell as cast weighed 11.075 tonnes, and over 1.4 tonnes of metal was removed in the course of the experiments.
Alan Buswell provided the tuning figures for this bell from the Gillett and Johnston books. The ‘as tuned’ figures were verified against four recent recordings of the bell and a good correspondence was found. Three sets of figures are given: as cast; the ideal figures showing what G & J were attempting to achieve in the tuning; and after tuning. The figures are given as intervals plus the variation from the (just-tuned) intervals in cents:
| Partial | Interval | As cast | Ideal | As tuned |
|---|---|---|---|---|
| Hum | Two octaves down | +50 cents | 0 cents | -53 cents |
| Prime | One octave down | +88 cents | 0 cents | -41 cents |
| Tierce | Minor third | +16 cents | 0 cents | -21 cents |
| Quint | Fifth | +99 cents | 0 cents | -21 cents |
| Nominal | Datum | Datum | Datum | Datum |
| Superquint | Fifth above nominal | -20 cents | 0 cents | +4 cents |
| Octave Nom. | Octave | +34 cents | 0 cents | +71 cents |
| I-7 | Eleventh | -9 cents | 0 cents | +39 cents |
| I-8 | Thirteenth | -44 cents | – | +24 cents |
| I-9 | Double octave | -17 cents | 0 cents | +60 cents |
These figures show that the extensive tuning work, intended to bring the upper partials to exact intervals, has instead only served to sharpen them all together as the bell was thinned. At the same time, the lower partials (hum, prime, tierce and quint) have flattened considerably; the hum for instance ended up half a semitone flat. It is illuminating to plot the figures before and after tuning in the same manner as previously (the ‘before’ data points are on the left):
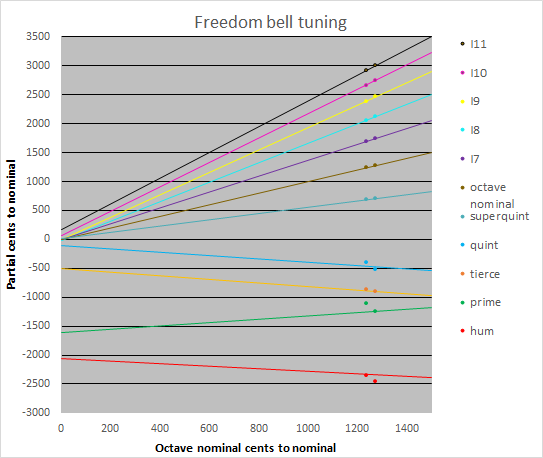
It is clear from this plot that the upper partials, and the tierce, have moved inexorably along the regression lines as the tuning took place. My research shows that the ‘ideal’ figures sought by Gillett and Johnston could not have been achieved.
The effect of these experiments on the sound of the bell was unfortunate. The hum and prime are sufficiently low in frequency as to have no effect on the timbre of the bell. However, the sharpening of the I-7 partial means that the secondary strike note of the bell is rather more than a fourth sharp of the primary strike, giving the bell an edgy tone. The bell before tuning, despite its sharp prime, probably sounded better than the final result.