Almost all musical instruments (such as pianos, organs, orchestral instruments and the human voice) have sounds that contain a range of frequencies f, 2f, 3f, 4f and so on where f is the lowest frequency in the sound. The pitch or note we asssign to the sound corresponds to the frequency f. Frequencies with this regular arrangement are called harmonic. The frequencies in the sound of bells, on the other hand, are not harmonic, and the pitch we assign to the sound of a bell is roughly an octave below the fifth partial up ordered by frequency. This partial is called the nominal, because it provides the note name of the bell. There often isn’t a frequency in the bell’s sound corresponding to the pitch we hear. This paradox has been known since the multiple frequencies in bell sounds were first recognised and measured. Lord Rayleigh investigated and confirmed the paradox in experiments on a Mears and Stainbank bell in 1890.
The explanation for this paradox is that the pitch we hear is generated in the ear, aural nerve or brain of the listener. The technical term for this is virtual pitch. Experiments to confirm that the pitch of bells is a virtual pitch generated inside the listener’s head were first done in the late 1920s and later confirmed by other researchers, but the practical consequences of this for bellfounders and bell tuners had not been recognised when I began my PhD research in 2002. The research done as part of the PhD included experiments on people’s hearing and perception of pitch. As well as confirming virtual pitch as the origin of the strike pitch of bells, the experiments also demonstrated that the strike pitch, although approximately an octave below the nominal frequency, is also influenced by other frequencies in the bell. It showed that for very big and very small bells, partials other than the nominal determine the note we hear. For the majority of bells, neither large nor small, experiments showed that the note heard can differ from the nominal frequency by a quarter of a semitone. This is quite sufficient for a bell to sound out of tune despite its nominal frequency being exact.
The research involved analysis of the partial frequencies of over 2,000 bells from 15 countries, spanning 9 centuries, and cast by at least 100 different founders. (Since the completion of the PhD in 2008, work has continued and my collection of bell recordings now includes over 10,500 bells, including 308 steel bells – most bells are made from bronze). The PhD experiments included tests on the hearing of over 50 people. These pages give a brief overview of some of the results.
One experiment described in the thesis, undertaken by 17 people, investigated what note is heard in bells of different sizes with nominal frequencies ranging from 315Hz to 4000Hz. The results are shown in the first figure.
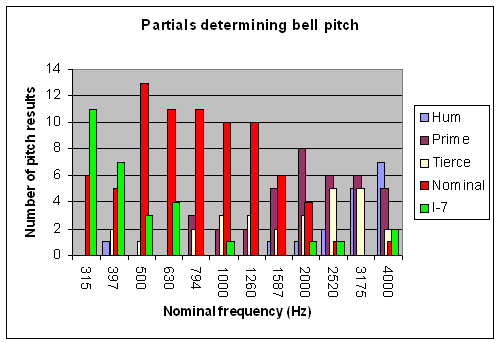
What this chart shows is that for bells with nominals between 500Hz and 1600Hz, i.e. weights from about 2 tonnes down to about 500 kg, most people hear a note based on the nominal partial. For heavier bells, the majority of people, by about two to one, hear a ‘secondary strike’ about a fourth higher than the nominal, based on upper partial I-7. For bells with nominals above 1600Hz, for most people the prime or hum partials define the note heard, and the nominal becomes irrelevant if its frequency is above 2500Hz. The thesis shows that the secondary strike is due to the way our ears work. There is nothing the bellfounder can do to remove it, though its pitch relative to the nominal can be altered by changing the design of the bell.
Another experiment, undertaken by 30 people over the internet, shows that for bells of middling size whose note is determined by the nominal, the exact pitch heard depends on the upper partials as well. In bells which are proportionally thick and heavy for their note (as is common in the trebles of peals of ten and twelve), the upper partials are squashed together, and this flattens the strike note. Thin bells have wider upper partials and sharper strike notes. The results of this experiment allow, for the first time, the shift in pitch to be calculated. The following figure, summarising the experimental results of all 30 people, shows how the pitch heard varies with the tuning of the octave nominal (which as will be shown on the next page, can stand proxy for all the upper partials), the prime and the tierce.
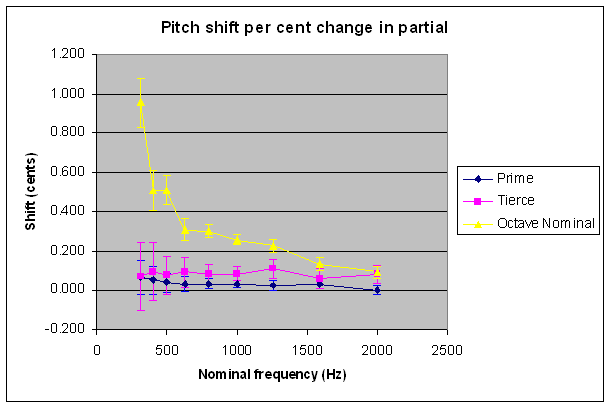
The plot shows the shift in the strike pitch, in cents (i.e. hundredths of a semitone), for a one cent shift in the relevant partial. At low nominal frequencies, the pitch observed depends very strongly on upper partial tuning, due to the secondary strike effect. At higher nominal frequencies, the pitch shift varies between 0.2 and 0.1 cents per one cent change in the octave nominal. Octave nominals in the range 1140 to 1280 cents are commonly encountered (though much sharper and flatter upper partials are seen in extreme cases). This range of 140 cents results in a pitch shift of between 14 and 28 cents (i.e. over 1/4 of a semitone). In the thesis, a simple model is fitted to the results to make them easy to use in practice.
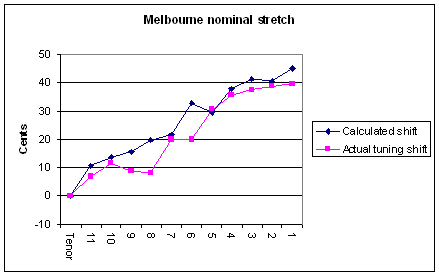
As a result of the pitch shift due to the octave nominal, the trebles of tens and twelves can sound flat and dull if they are too thick, even though their nominals are tuned exactly. From time to time, bellfounders have tried to compensate for this flat, dull sound by tuning the nominals of trebles sharp, known as stretch tuning. In the thesis, the actual tuning of a number of stretched peals of twelve is compared with the predictions from experiment. The second figure compares the actual and predicted stretch tuning of the 1889 Whitechapel 12 at St Paul’s Cathedral, Melbourne, Australia. The vertical scale is in cents. As can be seen, there is good agreement. The minor discrepancies are due to tuning errors rather than deficiencies in the model. The strike notes of the trebles in this peal are shifted from the nominal by almost half a semitone – large enough to be musically significant, but small enough that until now the effect has not been fully investigated.
Other areas covered in the thesis include an extensive survey of academic papers and books on bell acoustics, together with a comprehensive bibliography; investigation into the weights and upper partial frequencies of almost 2,000 bells to show that thicker bells have compressed upper partials; an investigation of the upper partials of over 2,000 bells showing for the first time that it is not possible to tune them independently; analysis of the partial frequencies of English and German steel bells; an account of the experimental tuning in 1950 by Gillett and Johnston of the 9.66 tonne Berlin Freedom bell in which they tried and failed to control its upper partials despite removing 1.4 tonnes of metal on the tuning machine; experiments to show that changes in the intensities of the nominal and upper partials do not affect the strike note; comparison of experimental results against various theories of pitch; translations of some historic documents in bell acoustics into English; and more.