(Since the original version of this article written in February 2022, it has been updated with several additional peals of historic bells, five Taylor peals, and a better approach to the analysis.)
This investigation was prompted by recent visits to peals of bells cast by William Dobson which have not been tuned since first installation (Burslem, Elland, Poole and Tyldesley). There are visible scratch tuning marks in bells in each peal, and yet the nominals in the smaller bells in these peals are well sharp of the musical scale. Why would a founder tune their bells but leave them sharp?
In another example, Tim Jackson of the Dove team sent me recordings of the 1877 Warner bells at Kirkby Stephen (included in this study) and in his email noted that the treble nominal was nearly half a semitone sharp. He said “I don’t recall them being so far out of tune . . . it takes me by surprise when the figures come out so differently from what I hear.”

The investigation into 31 historic peals of bells described in this article proves that they were tuned or assessed using strike notes, not nominal frequencies. The origin of the strike note in a bell is explained in the next section. Once the flattening effect on the strike note of other partial frequencies in the bells (particularly the upper partials) is taken into account, the accuracy of the strike pitches in these peals proves to be much better than expected. The upper partials of bells are not routinely recorded, so this accurate tuning of the strike notes in historic peals has not previously been recognised.
In investigating the strike notes of these bells, we are investigating the hearing of the bellfounders who cast and tuned them, and in particular what note they heard when a bell was rung.
Taylors returned to tuning by strike notes between the 1950s and 1970s as described in another article on this site. Five Taylor peals tuned by strike note were also included in this investigation and their tuning proves to be remarkably consistent with the historic peals.
Partial frequencies and the strike note
The sound of an individual bell is made up of a number of frequencies or partials. The lowest five partials are the hum, prime, tierce, quint and nominal. In a true-harmonic bell (as most modern bells are) the hum, prime and nominal are in exact octaves. In an old-style bell, the hum is commonly sharp and the prime is flat. These five partials are the ones commonly measured for bells but above the nominal there are more frequencies – the upper partials – which have a significant influence on the sound of the bell.
The strike pitch or strike note, which is the note that we hear when a bell rings, is generated in the ear from the nominal and upper partials. This is important; the note we hear doesn’t necessarily correspond with any of the partial frequencies that can be physically measured. The strike note is approximately an octave below the nominal, but my PhD research showed that the exact note is significantly influenced by the upper partials, and also to some extent by the prime. If a bell is thick and heavy the upper partials are flattened and this flattens the note we hear.
The notes of modern bells are tuned by adjusting the nominal frequencies to the musical scale. Historic founders may not have know how to measure individual partials. Instead, this paper shows that bells were tuned together according to their strike notes. Whether the strike notes of a peal of bells are in tune with one another can only be determined by comparing the notes heard against some other musical instrument. There is to my knowledge almost nothing in the written record on how these historic peals were tuned together or how the tuning discrepancies in a peal were assessed. The main evidence we have is the bells themselves.
This paper is in two parts. First, the evidence from the peals of bells is presented. Then, what evidence I am aware of on historical tuning methods is reviewed in the light of this analysis.
The historic peals
To test the hypothesis about tuning with strike notes, I searched my library of bell recordings for peals of 8 or 10 which:
- were cast by the same founder
- were cast prior to the adoption of tuning nominals against tuning forks
- have not been retuned since first installation (identified by investigation of the history of the bells, inspection of the bells for tuning marks, or where it is clear from the partial frequencies that the bells have not been tuned).
The investigation used peals of eight or ten to include a significant difference in note between largest and smallest bells. This helps reduced the impact of measurement and tuning errors by spreading them across a greater range of frequencies.
Almost all the peals in my collection of bell recordings meeting these criteria showed similar stretch, apart from a small number (generally from Taylors in the late 19th century) which seemed to follow different principles, and were excluded from the analysis. The figures for four peals (Gloucester, Liversedge, Wisbech and Wrexham) are those measured by Taylors prior to retuning, kindly researched for me by Chris Pickford. For these four peals, the octave nominal interval was taken from recent recordings; this interval is not much affected by the retuning.
The original version of this analysis included only peals from a single founder with the same casting date. It has now been expanded to include peals from the same founder cast in multiple years, and five stretched Taylor peals from the 20th century. The conclusions are unchanged.
The founders and dates of the 31 historic peals and five Taylor peals investigated are as follows:
| Founder | Peals and dates |
|---|---|
| Historic peals | |
| Barwell | Blakenhall 1897, Northampton 1897 |
| Briant | Condover 1812/1813 |
| Dobson | Ashbourne 1815, Elland 1825, Liversedge 1815, Poole 1821, Wisbech 1823 |
| Lester / Pack / Chapman | Ewell 1767/1830/1890, Shifnal 1770/1771, Mancroft 1775 (back ten) |
| Mears | Borden 1802, Chelsea 1824, Drayton 1871/1880, Pimlico 1849, Ranmore 1859, Steyning 1889, Stockport 1897, Warfield 1913, Wargrave 1915, Epsom 1920 |
| Rudhall | Bristol All SS 1727, Gloucester St Mary 1710/1749/1772, Lichfield 1726/1734, Painswick 1731/2, Tetbury 1727/1803, Wrexham 1726/1728/1737 |
| Warner | Kirkby Stephen 1877, Settle 1887, Warminster 1881, Wellington NZ 1879 |
| 20th century peals | |
| Taylor | Cambridge St Andrew 1956, Chester Cathedral 1973 (back ten), East Retford 1968, Houston 1971, Tewkesbury 1962 (back ten) |
The temperament in which the nominals were tuned for the 31 historic peals was assessed. On average across all the peals the closest fit was a temperament with slightly flattened 3rds, 6ths and 7ths, between meantone and equal temperament. The five 20th century Taylor peals were tuned in equal temperament.
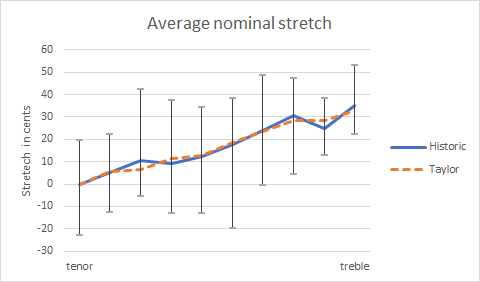
The chart shows the average, maximum and minimum nominal deviations for each bell. The successive sharpening of the bells from tenor to treble is clear. The trebles of eight and ten are stretched by up to a third of a semitone. The values for the 20th century Taylor peals are very consistent with the historic peals.
Stretch tuning is not to everyone’s taste. In particular, some people with perfect pitch or experience in listening to bell partials hear the nominal frequencies, not the strike notes, and dislike how sharp they are. But this investigation shows that historic founders and Paul Taylor heard strike notes in a consistent fashion.
The average, maximum, minimum and standard deviation of the divergence of the nominal from equal temperament compared with the average for all 36 peals is as follows:
| Bell | Average | Maximum | Minimum | Std. Dev. |
|---|---|---|---|---|
| treble of 10 | 34.7 | 53.1 | 22.1 | 8.4 |
| 2 | 25.5 | 38.2 | 13.0 | 7.2 |
| treble of 8 | 30.5 | 47.0 | 4.5 | 9.6 |
| 4 / 2 | 24.0 | 48.4 | -0.7 | 10.2 |
| 5 / 3 | 17.9 | 38.1 | -19.7 | 13.2 |
| 6 / 4 | 12.2 | 34.0 | -13.0 | 12.5 |
| 7 / 5 | 9.3 | 37.2 | -13.3 | 11.2 |
| 8 / 6 | 9.9 | 42.5 | -5.5 | 10.8 |
| 9 / 7 | 5.2 | 22.0 | -12.6 | 8.3 |
| tenor | 0.0 | 19.4 | -22.9 | 8.9 |
In the row for the trebles of eight, the average sharpening is 30.5 cents and the standard deviation indicates that we expect 68% of all trebles to have a nominal sharp by 30.5 ± 9.6 cents. For the trebles of ten, 68% of all trebles have a nominal sharp by 34.7 ± 8.4 cents. So this sharpening is significant, both statistically, and also musically – the average stretch across the peals is about 1/3 of a semitone. The stretch in the tenor is zero by definition, because the intervals have been calculated relative to the tenor nominal. There is a range of values for the tenor because the tenor can be out of tune with the rest of the peal.
If after casting a bell sounded out of tune with the remainder of the peal, the choices available to the founders of the historic bells were limited. They could recast the bell if it was significantly far out, scratch or file metal from the inside of the soundbow to flatten the bell, or skirt the bell (chop away the lip of the bell) to sharpen it. Rudhalls had a tuning machine capable of cutting metal from the inside of the sound bow which was built in the 1790s. The machine was moved to Whitechapel in the 1840s when the Gloucester foundry closed. The other founders did not have such aids.
Effect of octave nominal and prime on strike pitch
This stretch tuning of around 1/3 of a semitone in the octave can be explained if the founders were assessing bells by their strike pitch or note, not the nominal frequency. My PhD research (11) indicated that the strike note of a bell sounds flatter if the frequencies of the upper partials above the nominal, and in particular the interval from octave nominal to nominal, are flatter than average. The strike note also sounds a little flatter if the interval between prime and nominal is flatter than average. Peals of bells display differences in octave nominal tuning across the peal; the trebles in general are proportionally thicker and heavier than the tenors, which flattens their octave nominals. The flat octave nominal flattens the strike pitch below what would be expected from the nominal frequency alone. The historic peals also have trebles with flat primes, and this flat partial also depresses the strike pitch.
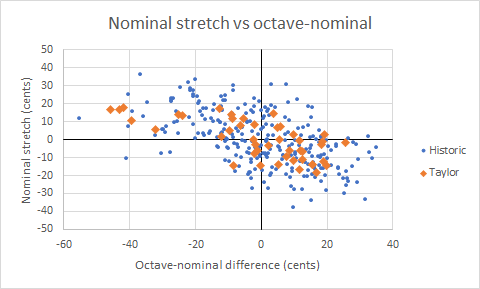
Here is a plot, for all 312 bells in the 36 peals, of the degree of stretch in the nominal compared with the tenor, against the octave nominal interval for each bell:
The plot below for the stretch against the prime interval only includes the 266 bells in the historic peals, as the modern Taylor primes are exact octaves:
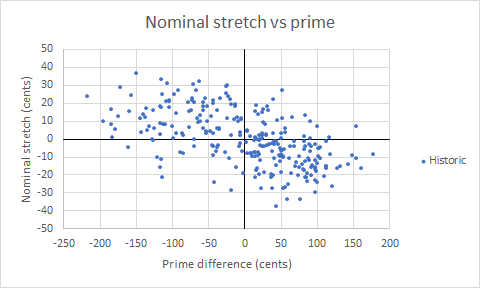
The horizontal axis is the interval from octave nominal to nominal in cents, or from prime to nominal in cents, between the bell of interest and the average for the whole peal. For both octave nominal and prime there is a clear linear relationship. Plotting the stretch against the tierce and hum tuning shows much less correlation, and the hum and prime were excluded from further analysis.
What these plots show is that bells with flatter octave nominals or flatter primes have sharper nominals. The flatter octave nominals or primes flatten the strike note of the bells affected, and the nominal is sharpened to compensate and bring the strike note back in tune with other bells in the peal.
The graph for octave nominals also shows that the effect is the same both in historic bells and in Taylor bells of the middle 20th century tuned with stretch.
The effect of the octave nominal and prime intervals is additive, in that smaller bells tend to have both flatter primes and flatter octave nominals. To separate out the effect of these two factors, a regression was done with the octave nominal and prime intervals as independent variables. The results of the regression are as follows:
- 43% of the variance in the nominal frequencies is due to the octave nominal and prime intervals. I interpret the remaining variance as tolerance of tuning inaccuracies, i.e. how far a bell could sound out of tune before it was rejected and recast
- For every 100 cents that the octave nominal of a bell is flatter than the tenor octave nominal, on average the bell’s nominal is stretched by 34.3 ± 4.0 cents
- For every 100 cents that the prime of a bell is flatter than the tenor prime, on average the bell’s nominal is stretched by 7.2 ± 0.9 cents.
It is useful to look at the residuals – the remaining variance in nominal tuning after the effect of octave nominal and prime differences is taken into account:
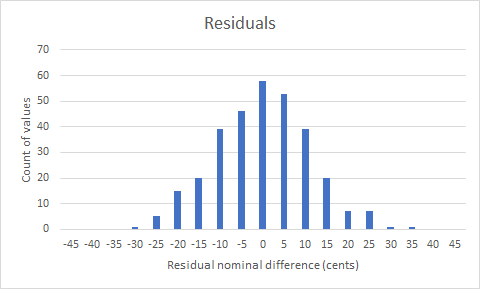
The standard deviation of the residuals is 10.9 cents. If the 20th century Taylor peals are excluded, the standard deviation only goes up to 11.3 cents. This means that 68% of the bells investigated have a nominal stretch within 11 cents of the value predicted by the octave nominal and prime tuning. As mentioned before, this can be interpreted as the tolerance of the bellfounders and their customers to tuning discrepancies. This compares with the commonly accepted tolerance of ±10 cents for modern change-ringing bells where the individual partials, rather than the strike notes, are tuned with forks or electronic equipment.
This analysis clearly demonstrates that the stretch in these peals is there to compensate for the thickness / relative weight of the trebles, and for flat primes. The bellfounders who cast these bells were assessing whether they were in tune based on their strike pitch – the virtual pitch effect – rather than by the nominal frequency of each bell. This is true both for the historic peals, and the 20th century Taylor peals. Despite some of the historic peals not sounding too good individually (due to sharp hums, flat primes and out-of-tune nominals), the peals show a closer tolerance of tuning across each peal than might be expected from initial inspection of the nominal tuning figures.
In one sense this conclusion is not a surprise. It was only with the advent of true-harmonic tuning that UK bellfounders began to measure the frequencies of individual partials. What is unexpected is the closeness of the nominal tuning once the factors leading to the stretch are taken into account.
(In the original version of this analysis, the intervals in cents of octave nominal and prime for each bell were taken relative to the tenor octave nominal and prime cents. The stretch in each bell’s nominal was taken as the interval in cents between bell nominal and tenor nominal, minus the temperament. This gave undue weight to the tenor tuning in each peal. In a peal of eight, the tenor tuning was eight times more likely to affect the results than any other bell. In the revised analysis, octave nominal and prime tuning are taken relative to the average across the peal. Stretch is assessed by calculating the equivalent tenor nominal for each bell by taking its nominal minus the temperament, and then assessing each bell against the average equivalent tenor nominal for the peal.)
Historic methods of bell tuning
I would like to thank Chris Pickford for his help with this section. Remaining errors and opinions are my own.
Bellfounders rarely documented how they worked, and there is very little written information on how the tuning of bells was assessed prior to the modern era, and most of it comes from secondary sources.
Before the advent of electronic tuners, keyboard, stringed and woodwind instruments were tuned using beats. The notes of these instruments have harmonic partials, and for example two notes an octave apart can be tuned by listening for beats between the fundamental of the higher note and the first overtone of the second. The roughness between slightly mis-tuned notes with a common overtone was used to tune instruments before the existence of multiple partials in a sound was recognised. A description of this approach to tuning was published in 1496, whereas the first written account of multiple partials in the notes of stringed instruments was published by Marin Mersenne in Harmonie Universelle in 1636, as explained on page 273 of Fletcher and Rossing Physics of Musical Instruments (1).
Bells have inharmonic partials, so the technique of beating or listening for roughness between overtones is not available to assist the tuning of one bell against another.
The earliest reference I know of to the fact that bells have multiple partial frequencies is in Isaac Beekman’s journal for 1633 (2). He writes about Jacob van Eyck, a blind carillon player who worked with the Hemony brothers to develop the techniques for true-harmonic tuning that enabled the Hemonys to dominate carillon production in the Low Countries in the 17th century. Van Eyck was able to demonstrate that bells and wineglasses had multiple partial frequencies of vibration. There is also a letter in 1633 from Isaac Beekman to Mersenne discussing the difficulty they both had in understanding how a physical body could vibrate with more than one frequency simultaneously (3).
Lehr in The Art of the Carillon in the Low Countries documents what is known about the Hemony’s tuning methods, quoting letters written by François Hemony in 1651 and Melchior Fokkens in 1662 (4). The Hemonys used tuned metal bars suspended from woollen threads to generate reference tones to tune against. It is suggested by Lehr that the bars were sprinkled with sand to show when they were resonating with a partial frequency in a bell, but this may be speculation. The Hemonys themselves wrote no further description of their methods, referring to their knowledge as “the bellfounder’s secret”.
The tuning fork was invented in 1711 by John Shore, trumpeter to the English Royal Court and an associate of Handel. Prior to this invention, pitch was generally determined by pitch pipes – small wind instruments similar to stopped organ pipes with a sliding stop calibrated with the notes generated. Tuning forks became the standard for pitch determination due to their stability and ease of use. Alexander Ellis in one of his appendices to Helmholtz’s On the Sensations of Tone refers to a pitch pipe of 1730 belonging to the bellfoundry Colbachini at Padua, and a set of tuning forks belonging to the bellfoundry Cavedini at Verona, supposed to be a century old (he was writing in 1877) (5).
Fred Sharpe in Church bells of Herefordshire gives a brief description of the Rudhall’s tuning machine, installed in their foundry at Gloucester and later moved to Whitechapel, and a drawing of it at Whitechapel (6). The tuning machine was probably built by the Rudhalls just before 1800. G. W. Counsel in The History and Description of the City of Gloucester, published in 1829, says the tuning machine was first used ‘about 30 years ago’ (7). According to the listing information for the Whitechapel Bellfoundry, the machine was installed there around 1848. The machine could cut the inside of the soundbow and partway down into the waist. I can find no description of how the machine was used – for example, whether it was used to tune nominal frequencies or strike pitches.
Mary Bliss in a 2003 paper in the Transactions of the Bristol and Gloucestershire Archaelogical Society (8) presents extracts from a notebook kept by John Rudhall between 1829 and 1835. It is clear from the notebook that John Rudhall was using a pitch pipe to determine the notes of bells – notes are given as ‘A pipe’, ‘just covered the mark above E pipe’ or ‘almost a quarter below B’. Mary asserts that these are strike pitches and although we now know this was correct, she does not explain the assertion.
Taylors on the other hand were using tuning forks from the 18th century. A letter from John William Taylor senior in 1865 to Canon Cattley at Worcester says ‘As regards tuning forks the majority of mine were made by my grandfather (Robert Taylor)’. (9) Chris Pickford believes that forks were in use by Arnold and the Eayres prior to the takeover by Robert Taylor in the 1780s, and that the evaluation of bell pitch was done by ear against the forks.
Taylors in the later 19th century, and all UK founders as they adopted true-harmonic tuning, used tuning forks to measure individual partial frequencies, just as the Hemonys did 200 years earlier with their tuning bars. The measurements were done either by counting beats between an individual partial and a fork with a frequency close to it, or placing the fork on the bell to see if there was a resonance. John Llewellin in his book Bells and Bellfounding published in 1879 describes how he used tuning forks to measure individual partials in a bell by placing them on the bell to stimulate resonance. (10)
Whitechapel continued to use tuning forks to measure strike pitches by ear into the 1920s. When Lord Rayleigh did his investigation into bell acoustics in 1890, Mears & Stainbank lent him a bell, together with a tuning fork tuned to its pitch. His experiments showed that the fork was tuned to the strike pitch, not the nominal. This fork must have been tuned by ear, as due to the flat prime of this bell, the fork did not match any of the partial frequencies. A further example of this practice occurs in a letter written by A. A. Hughes in December 1925 reporting on the old ten at Coventry. The figures he gives for the note of each bell, taken he says with specially tested forks, are for the strike pitches or half-nominals, not the nominals.
Richard Offen provided more detail on the Mears & Stainbank approach in a post to the Bell Historian’s list on 24 June 2006:
“[In 1897] Whitechapel were making a set of tuning forks for each ring they produced (I believe they still have all the sets in their archive). If I remember the process correctly, as related to me by Bill Hughes, forks were made to correspond to the strike note of each bell as cast. The tuning forks were then taken to a quiet corner of the foundry and ‘adjusted’ to give a set of forks that sounded in tune to the tuner. These forks were then used to adjust the strike note of each bell, presumably by ear and not by placing the fork on the bell to get sympathetic resonance. Bill Hughes always used to quote the note of a bell giving a frequency as half that of the nominal.”
This is confirmation that Whitechapel in the late 19th century were measuring strike pitches, not nominals, the same approach as used by the other founders investigated in the first section of this paper.
Towards the end of another article on stretch tuning, I show that Paul Taylor returned to the use of strike pitch to tune the nominals of Taylor bells between the 1950s and 1970s. Mike Milsom, who worked with Paul Taylor for part of this period, tells me that Paul didn’t explain how he decided on the degree of stretch required in a peal. This investigation shows the he was following the same approach as the historic bellfounders investigated here.
References
(1) Fletcher N. H. and Rossing T. D., The Physics of Musical Instruments, 2nd edition, Springer (1998)
(2) Beeckman, I., (ed. De Waard, C.), Journal tenu par Isaac Beeckman, Tome Triosième, 1627-1634, Martinus Nijhoff, La Haye (1945)
(3) Beeckman, I., (ed. De Waard, C.), Journal tenu par Isaac Beeckman, Tome Quatrième, 1627-1634, Martinus Nijhoff, La Haye (1953)
(4) Lehr, André, The Art of the Carillon in the Low Countries, Lannoo, 1991 p.132
(5) Helmholtz, Hermann, On the Sensations of Tone, Dover Publications, 1954 p.484
(6) Sharpe, Fred, Church Bells of Herefordshire, Smart and Company, 1975 vol. 5 p. 702
(7) Counsel, G. W., The History and Description of the City of Gloucester, J. Bulgin 1829 p.218
(8) Bliss, Mary, The Last Years of John Rudhall, Bellfounder of Gloucester 1828-35, Transactions of the Bristol and Gloucester Archaeological Society 2003, Vol. 121, 11-22 or on the society website
(9) Letter from JWT (senior) to Canon Cattley, Worcester, 4 May 1865 (Taylor archive 6/1/2/25 pp.151-2)
(10) Llewellin, John, Bells and Bellfounding, Arrowsmith, Bristol 1879 or on the Whiting Society website
(11) W. A. Hibbert, The Quantification of Strike Pitch and Pitch Shifts in Church Bells, PhD thesis, April 2008, pp.195-197